I can't figure this one out
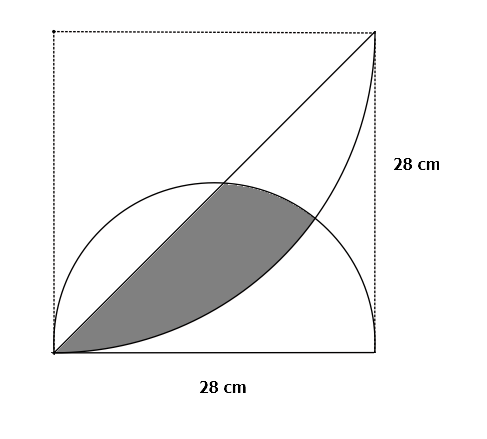 Find the area of the shaded region to two decimal places.
Find the area of the shaded region to two decimal places.
The answer is 132.56.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
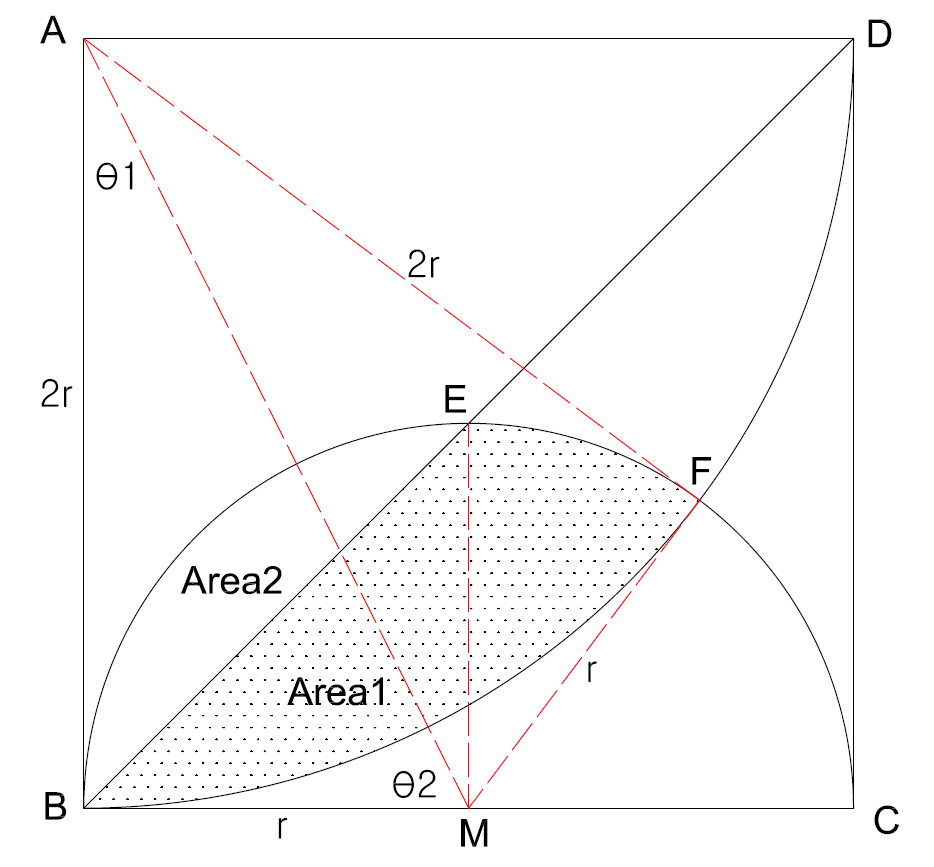
1) Put "M" in the mid point on the line "BC" and "F" in the intersection point between arc "BD" and "BC".
2) Make the line "AM", "AF", "MF", "ME"
3) The [Area1] + [Area2] = Fan area "ABF"+ Fan area"MFB" - Kite area "ABMF"
(∵ A ∪ B = A + B - (A ∩ B) )
4) Kite area "ABMF" = 2 × Triangle area "ABM"
(∵ Triagle "ABM" = "AMF" , due to the same of 3 sides)
5) The [Area2] = Fan area "MEB" - Triangle area"MEB"
6) So, we could derive the [Area1] [Area1] = Fan area "ABF" + Fna area"MFB" - 2 × Triangle area "ABM" - Fan area "MEB" + Tiangle area "MEB"
= 1/2×(2r)^2×2×Θ1 + 1/2×r^2×2×Θ2 - 2×1/2×(2r)×r - 1/4×π×r^2 + 1/2×r^2
= 3×r^2×Θ1 + 1/4×π×r^2 - 3/2×r^2 (∵θ1 + θ2 = π/2)
= r^2×{3×Θ1 + 1/4×π - 3/2}
7) Finally, we could find the [Area1] with r=14cm, (θ1 = Tan-1(1/2) ≒ 0.46365 rad, with a calculater)
[Area1] = 14cm×14cm×{3×0.46365 + 1/4×π - 3/2} = 132.56cm^2
I'm not good at writing in Web. so, It's too hard for me to write a mathematical formula in the solution. please excuse my solution.
i have see many solutions without the approach of calculus ,amazing... ,i personally use coordinate system +calculus to solve
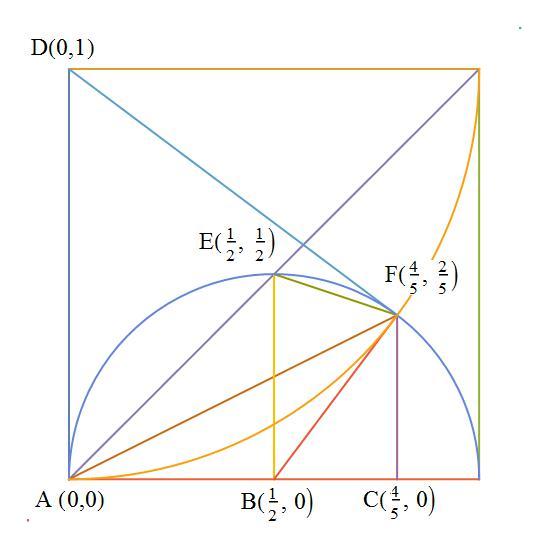
This depends on the fact that the arcs are orthogonal at point F. First, we rescale the square to an unit square. Then we have
Arc angle D = A r c T a n ( 5 4 3 5 )
Arc angle B = A r c T a n ( 1 0 3 2 5 )
From these, we can compute the areas of circle segments A F and E F
A F = 2 1 D − S i n ( 2 1 D ) C o s ( 2 1 D )
E F = ( 2 1 ) 2 ( 2 1 B − S i n ( 2 1 B ) C o s ( 2 1 B ) )
Next, we compute the area of triangle A E F
A E F = 2 1 ( 2 1 2 1 + 1 0 3 ( 2 1 + 5 2 ) − 5 4 5 2 )
Combining all and rescaling back to square of side length 2 8 , we have
2 8 2 ( A F + E F + A E F ) = 1 3 2 . 5 6 3 . . .
Let the lower left corner of the square be the origin O ( 0 , 0 ) and let the sides of the square lie along the positive x and y -axes. Next, label the other corners of the square P ( 0 , 2 8 ) , Q ( 2 8 , 2 8 ) , R ( 2 8 , 0 ) , and let M ( 1 4 , 0 ) be the center of the semicircle. Also, the semicircle and diagonal meet at S ( 1 4 , 1 4 ) .
Now to find the point other than O where the semicircle and quarter-circle meet can be determined by solving, simultaneously, the equations
( x − 1 4 ) 2 + y 2 = 1 4 2 and x 2 + ( y − 2 8 ) 2 = 2 8 2 .
Expanding these equations gives us that
x 2 − 2 8 x + y 2 = 0 and x 2 + y 2 − 5 6 y = 0
⟹ 2 8 x = 5 6 y ⟹ x = 2 y ⟹ 5 y 2 = 5 6 y ⟹ y = 5 5 6 , x = 5 1 1 2 .
So label this point of intersection T ( 5 1 1 2 , 5 5 6 ) .
So now we need to find the area of the shaded region O S T . To do this geometrically, we need to add the areas of the following three subregions:
-
(i) the triangle Δ O S T ;
-
(ii) the sector P O T minus the triangle Δ P O T ;
-
(iii) the sector M S T minus the triangle Δ M S T .
For (i), we can use the standard distance-between-points formula to find that
∣ O S ∣ = 1 4 2 , ∣ S T ∣ = 5 1 4 1 0 , ∣ O T ∣ = 5 5 6 5 .
Using Heron's formula we find that the area of Δ O S T is 7 8 . 4 0 0 . . . .
For (ii), we note first that ∠ O P T = tan − 1 ( 3 4 ) . Next, we note that the area of Δ P O T is 2 1 ∗ 2 8 ∗ 5 1 1 2 = 5 1 5 6 8 . Thus the area of subregion (ii) is
2 1 ∗ 2 8 2 ∗ tan − 1 ( 3 4 ) − 5 1 5 6 8 = 3 9 2 tan − 1 ( 3 4 ) − 5 1 5 6 8 = 4 9 . 8 9 9 7 . . . . .
For (iii), we note first that ∠ S M T = tan − 1 ( 4 3 ) . Next, we note that the area of Δ M S T is 2 1 ∗ 1 4 ∗ ( 5 1 1 2 − 1 4 ) = 5 2 9 4 . Thus the area of subregion (iii) is
2 1 ∗ 1 4 2 ∗ tan − 1 ( 4 3 ) − 5 2 9 4 = 9 8 tan − 1 ( 4 3 ) − 5 2 9 4 = 4 . 2 6 3 . . . .
Adding the areas of these three subregions gives us a total area of the shaded region of 7 8 . 4 0 0 + 4 9 . 9 0 0 + 4 . 2 6 3 = 1 3 2 . 5 6 3 to 3 decimal places.
Use coordinate geometry and some calculus.
Big circle with radius 28: x^2+(y+28)^2=28^2 = 28-sqrt(784-x^2)
Small circle with radius 14: (x-14)^2+(y^2=14^2= sqrt(28x-x^2)
If you are not sure how to formulate circle equation, refer to circle equation.
Find intersection points between two circles: Set both equation equal to each other and we get ( 0,0) and ( 112/5, 56/5)
Now we calculate areas
area a= Intergate sqrt(28x-x^2) from 28 to 112/5 = 43.835
area b= Integrate 28-sqrt(784-x^2) from 112/5 to 0 = 75.540
area c= 14^2- Integrate sqrt(28x-x^2) from 0 to 14= 196- 153.94= 42.06
area d= right triangle of (14*14)/2 - 42.06 = 55.94
area e= what the question seek= small semi circle- ( a+b+d)= 307.87- ( 43.835+ 75.540+55.94)= 132.561
The needed are is [ C O P N ] = a + b + c .
a = 2 1 ( [ Sector A B C ] − [ △ A C O ] ) = 2 1 ( 4 2 8 2 π − 2 2 8 2 ) = 1 1 1 . 8 7 6 0 8 0 1 c m 2
To find b and c , let us assign coordinates as follows:
\(\begin{array} {} A(-14,14) & B(14,14) & C(14,-14) & D(-14,-14) \\ M(0,-14) & O(0,0) & P(x,y) & N(14(\sqrt{2}-1),-14(\sqrt{2}-1) \end{array} \)
Since P ( x , y ) is the meeting point of the circles:
⇒ { x 2 + ( y + 1 4 ) 2 ( x + 1 4 ) 2 + ( y − 1 4 ) 2 = 1 4 2 = 2 8 2 . . . ( 1 ) . . . ( 2 )
Eq. 2 − Eq. 1: 2 8 x + 1 4 2 − 5 6 y = 2 8 2 − 1 4 2 ⇒ x = 2 y + 1 4
Substituting in Eq. 1:
4 y 2 + 5 6 y + 1 4 2 + y 2 + 2 8 y + 1 4 2 = 1 4 2
⇒ 5 y 2 + 8 4 y + 1 9 6 = 0 ⇒ y = − 2 . 8 ⇒ x = 8 . 4
We note that the area of sector A P N = b + c + d . Let ∠ P A N = 2 θ . Then, b + c + d = 2 8 2 θ . We also note that:
sin θ = 2 8 2 1 P N = 5 6 [ 8 . 4 − 1 4 ( 2 − 1 ) ] 2 + [ − 2 . 8 + 1 4 ( 2 − 1 ) ] 2 = 0 . 0 7 0 8 8 9 0 2 ⇒ θ = 0 . 0 7 0 9 4 8 5 2 7 r a d
Therefore,
b + c + d = 2 8 2 ( 0 . 0 7 0 9 4 8 5 2 7 ) = 5 5 . 6 2 3 6 4 5 4
b = 5 5 . 6 2 3 6 4 5 4 − ( c + d ) = 5 5 . 6 2 3 6 4 5 4 − 2 1 ˙ 1 4 2 ˙ 2 8 sin 2 θ = 5 5 . 6 2 3 6 4 5 4 − 3 9 . 2 = 1 6 . 4 2 3 6 4 5 4
To find c , let ∠ O M P = 2 ϕ
sin ϕ = 1 4 2 1 O P = 2 8 8 . 4 2 + ( − 2 . 8 ) 2 = 0 . 3 1 6 2 2 7 7 6 6 ⇒ ϕ = 0 . 3 2 1 7 5 0 5 5 4 r a d
Area of sector M O P = 1 4 2 ϕ = 6 3 . 0 6 3 1 0 8 6 6
c = 6 3 . 0 6 3 1 0 8 6 6 − [ △ M O P ] = 6 3 . 0 6 3 1 0 8 6 6 − 1 4 2 sin ϕ cos ϕ = 6 3 . 0 6 3 1 0 8 6 6 − 5 8 . 8 = 4 . 2 6 3 1 0 8 6 6 2
Therefore, the shaded area:
= a + b + c = 1 1 1 . 8 7 6 0 8 0 1 + 1 6 . 4 2 3 6 4 5 4 + 4 . 2 6 3 1 0 8 6 6 2 = 1 3 2 . 5 6 c m 2