I can't solve it myself.

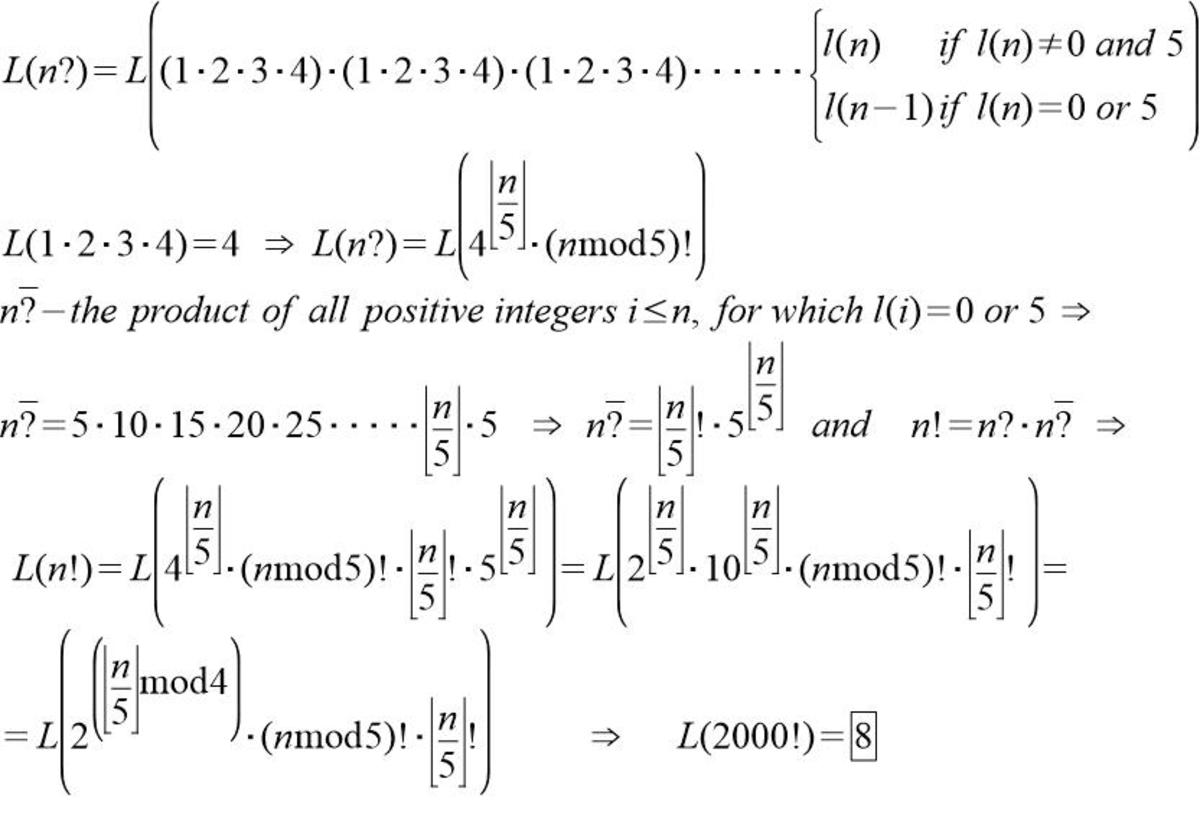
There are some interesting discussions of the general sequence of last non-zero digits of $n!$ at the OEIS, here .

If you're just interested in a way to find the last non-zero digit of $2000!$ , we can do it with an algorithm.

First, it's worth noting that simply computing $2000!$ is not the way to go. It is - obviously - huge, and has many more digits than we're interested in. However, it's fairly easy to compute the last $k$ digits of $2000!$ algorithmically; we just calculate the sequence $a_1=1$ , $a_{n}=\text{Mod} \left(n a_{n-1},10^k \right)$

where $\text{Mod} (p,q)$ is the remainder when $p$ is divided by $q$ .

How many digits do we need to retain for $2000!$ ? We quickly start adding zeros onto the end of the factorials; in fact, $2000!$ has $499$ ending zeros, so we could do this with $k=500$ . But this is still a huge calculation.

We can reduce the number of digits needed by ignoring ending zeros.

Now note that the number of ending zeros of $n!$ increases exactly when $n$ is a multiple of $5$ (why is this?). If $n$ is a multiple of $5$ , but not $25$ , $n!$ has one more ending zero than $(n-1)!$ . If $n$ is a multiple of $25$ , but not $125$ , $n!$ has two more ending zeros than $(n-1)!$ , and so on.

So we need to know the highest power of $5$ that divides $n$ . This is usually written as $\nu_5 (n)$ .

The largest power of $5$ less than $2000$ is $5^4=625$ . So $625!$ has $4$ more ending zeros than $624!$ , and this is the worst case. Therefore we need to retain just $5$ ending digits - ie we need $k=5$ .

Finally, we can modify the sequence above as follows: let $a_1=1$ and $a_{n}=\frac{1}{10^{\nu_5 (n)}} \text{Mod} \left(n a_{n-1},10^5 \right)$

This is easy to implement in code (or Excel), and will give the correct final non-zero digit of $n!$ for all $n<5^5=3125$ . In particular, we find the last non-zero digit of $2000!$ is $8$ .

Hopefully this makes sense as a simple(ish) approach - there are much deeper discussions in the site linked above.

Well i noticed that the last digit in 10! Is 8

• And for make it easy! Lets say L(x)=the last non zero digit

Because L(10!)=8 So L((2×10)!)=L( $8^2$ )=4

L((3×10)!)=L( $8^3$ )=L(512)=2

Obviously that mean

• $\boxed{L((n×10)!)=L((8^n))}$ , Notice that $\boxed{L(8^{5})=8}$ so we back again from we start

Now we can get $\color{#D61F06}{L(2000!)}$

• L(2000!)=L((200×10)!)=L(( $8^{200}$ notice that 200 is divisible bye 5, so we back again to L(8^5) Which is =8

• So $\boxed{L(2000!)=8}$