I can't take this Heat!
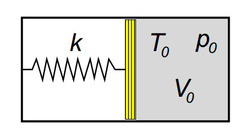 A system consists of two chambers, one is filled with a gas of molecules
(
P
o
,
V
o
,
T
o
)
while, the other chamber is
vacuum
. The Piston is held by a
spring
.
A system consists of two chambers, one is filled with a gas of molecules
(
P
o
,
V
o
,
T
o
)
while, the other chamber is
vacuum
. The Piston is held by a
spring
.
Find the heat capacity C ( in J/K ) of the system, such that when the gas is released, the piston touches the right wall and the spring is relaxed.
Details and Assumptions:
∙
The gas is
Monoatomic
in nature.
∙
P
o
=
1
.
5
a
t
m
∙
V
o
=
3
.
5
L
∙
T
o
=
2
2
7
o
C
∙
k
=
1
5
0
N
/
m
The answer is 2.1278.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Will it be in equilibrium as you said?
The compression in the spring at an instant can be given as x = A V x 0 = A V 0
Lets's assume the process is a quasi-equilibrium process. Therefore the pressure in the gas at any instant is the pressure exerted by the spring P . A = k ( A V ) . Now from gas equation P V = m R T ( k A 2 V ) V = m R T V 2 = k m R A 2 T
Work done by gas = work done by spring 2 1 k ( x 2 − x 0 2 ) = 2 1 k ( A 2 V 2 − A 2 V 0 2 ) = 2 1 k ( A 2 k m R A 2 T − A 2 V 0 2 ) = 2 1 m R T − 2 1 A 2 k V 0 2
From 1st law : △ U = Q i n − W o u t Q i n = △ U + W o u t Q i n = 2 3 m R ( T − T 0 ) + ( 2 1 m R T − 2 1 A 2 k V 0 2 ) Q i n = 2 3 m R T + 2 1 m R T + c o n s t a n t
H e a t c a p a c i t y = d T d Q i n = 2 3 m R + 2 1 m R = 2 m R = 2 T 0 P 0 V 0 ( i n S . I u n i t s ) = 2 . 1 2 8 J / K
@Rahul Badenkal why i am not able to get the answer by method if i use p=kx/a and then v=ax now on dividing the p and v , we got p/v=constant , and then treat this as polytropic process and apply the formula of c for that case ?
Log in to reply
Okay. If the process undergone by the gas is p/v=c(constant), then work done=pdv. Integrate that by substituting p=cv, between limits Vo to V. You get W = pV/2 - poVo/2 = mRT/2 - poVo/2.
Now dU = mcdT or deltaU = 3/2mc(T-To).
Now Qin = 3/2mc(T) + mRT/2 - poVo/2 - 3/2mcTo
So dQin/dT = 2mR = 2poVo/To.
https://brilliant.org/profile/nishant-1e4wj4/sets/target-jee-advanced-physics/293774/problem/a-classical-mechanics-problem-by-nishant-rai-3/ ( i am using the @Nishu sharma's method there )
yar shit i thought it to be specific heat capacity.
It's a polytropic process with n = -1.
As kx = PA and V is directly proportional to x and hence P V − 1 = c o n s t a n t