Chipped off square

Geometry Level 1

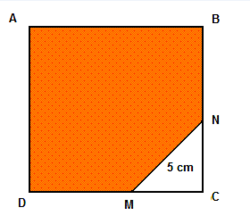The size of the perimeter of the square ABCD is equal to 100 cm. The length of the segment MN is equal to 5 cm and the triangle MNC is isosceles. Find the area of the pentagon ABNMD.

8000 square m 600 square cm 618.75 square cm 339.78 square cm

2 solutions

Michael Fuller
Apr 8, 2015

First we find the area of $ABCD$ :

Side length: $\frac { 100 }{ 4 } =25$

Area: ${ 25 }^{ 2 }={ 625cm }^{ 2 }$

Then we find the area of $MNC$ , which is a right angled isosceles triangle:

Using Pythagoras: ${ 5 }^{ 2 }={ \left( \overline { NC } \right) }^{ 2 }+{ \left( \overline { MC } \right) }^{ 2 }$

so $\overline { NC } =\overline { MC } =\sqrt { 12.5 }$

$\frac { { \left( \sqrt { 12.5 } \right) }^{ 2 } }{ 2 } =\frac { 12.5 }{ 2 } ={ 6.25cm }^{ 2 }$ (area $MNC$ )

Area $ABNMD$ : ${ 625cm }^{ 2 }-{ 6.25cm }^{ 2 }=\boxed { { 618.75cm }^{ 2 } }$

The solution can be slightly simplified by realizing you dont need to calculate the length of the sides.

$5^2cm^2=2x^2$ Area of the triangle= $1/2(base)*(height)=x^2/2$

So the area of the triangle is $25/4cm^2=6.25$ so the area of the pentagon, $ABNMD=((100/4)^2-6.25)cm^2=\boxed{618.75cm^2}$

Scott Ripperda - 6 years, 1 month ago

that's correct

Tootie Frootie - 6 years, 2 months ago

Sanjoy Roy
Apr 9, 2015

answer should be 623.75 sqr cm

triangle MNC isiso-scaled so 2x^2=5 the area of this triangle is 1.25 so 625-1.25 = 623.75

the area of triangle is 6.25 cm square i think you should check it again and focus your attention on the language of problem

Tootie Frootie - 6 years, 2 months ago

Chipped off square

2 solutions

0 pending reports