I don't know why its not easy...
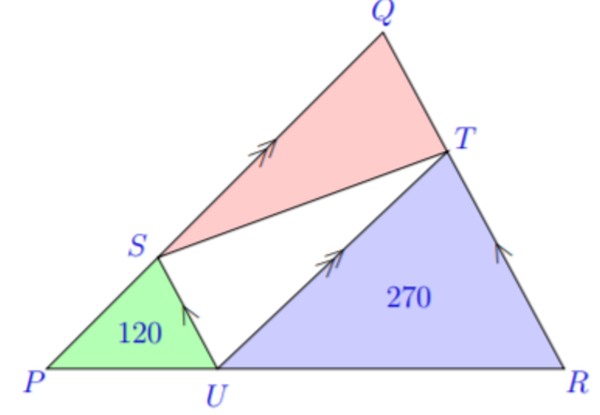
In △ P Q R , U is a point on P R , S on P Q , and T on Q R with U S ∣ ∣ R Q , and U T ∣ ∣ P Q . The area of △ P S U is 120 and that of △ T U R is 270. What is the area of △ Q S T ?
Source: AMC 2018 intermediate division
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Syed Hamza Khalid solution of "https://brilliant.org/discussions/thread/how-to-approach-this-question/?from_notification=14176037#comment-a3f5142823e92"
plz do check it!
Log in to reply
Thank you so much... its perfect ... loved it ... especially the diagram
We note that △ P S U , △ T U R , and △ P Q R are similar. Then
P U 2 U R 2 ⟹ P U U R = 1 2 0 2 7 0 = 4 9 = 2 3
Now, we have:
[ P S U ] [ P Q R ] ⟹ [ P Q R ] = P U 2 P R 2 = ( P U P U + U R ) = ( 1 + 2 3 ) 2 = 4 2 5 = 4 2 5 [ P S U ] = 4 2 5 × 1 2 0 = 7 5 0 [ ⋯ ] denotes the area of ⋯ .
we note that:
[ Q S T ] = 2 [ Q T U S ] = 2 [ P Q R ] − [ P S U ] − [ T U R ] = 2 7 5 0 − 1 2 0 − 2 7 0 = 1 8 0
There are many similar triangles in this diagram: △ S U P , △ T R U , and △ Q R P are all similar to each other, thanks to the two pairs of parallel lines.
Now the ratio of the areas of two similar triangles is the square of the ratio of the side lengths of the corresponding sides. Let A denote the areas of the various shapes. Thus, since A ( △ S U P ) = 9 4 A ( △ T R U ) , it follows that U P = 3 2 R U . Thus U P = 5 2 R P , and 1 2 0 = A ( △ S U P ) = 2 5 4 A ( △ Q R P ) , and A ( △ Q R P ) = 7 5 0 .
After subtracting the areas of △ S U P and △ T R U , we see that the area of the parallelogram S Q T U is 7 5 0 − 1 2 0 − 2 7 0 = 3 6 0 . The two triangles △ S Q T and △ T U S are congruent and thus the area of each is 1 8 0 .