I don't think I can do it
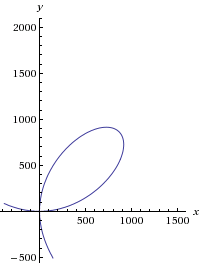 Find the area of the figure bounded by the curve
x
3
+
y
3
=
1
7
2
9
x
y
.
Find the area of the figure bounded by the curve
x
3
+
y
3
=
1
7
2
9
x
y
.
If the answer comes as B A 2 where A and B are co-prime positive integers. Find A + B .
The answer is 1735.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I like your solution very much! I got a way of deriving the parametrization that you used before, by converting the equation x 3 + y 3 = 3 a x y into polar coordinates first, so we get r = cos 3 θ + sin 3 θ 3 a sin θ cos θ . for 0 ≤ θ ≤ 2 π . Then using the equations x = r cos θ , y = r sin θ , we obtain x = cos 3 θ + sin 3 θ 3 a sin θ cos 2 θ and y = cos 3 θ + sin 3 θ 3 a sin 2 θ cos θ Then dividing in each fraction the denominator and numerator by cos 3 θ . Then we get x = 1 + tan 3 θ 3 a tan θ and y = 1 + tan 3 θ 3 a tan 2 θ Now you can get the parametrization by making t = tan θ , and of course when 0 ≤ θ < 2 π , we have 0 ≤ t < ∞ . Is there any other way of deriving it?
Log in to reply
This is a very lucid and elegant explanation, as one would expect from a Cuban- and Soviet-trained mathematician. Thank you!
Log in to reply
Otto, I really appreciate you compliment, but, believe me, I am nothing compared to you. I am always learning from your solutions, and I am being sincere: you are a great professor and mathematician.
@Otto Bretscher sir... Well I didn't do this problem complete but I sought it(I am lazy at calculations sorry!!) As we know that the curve is symmetric about line y=x we can apply transformation on y=(X+Y)/√2 and x=(X-Y)/√2 which gave us an explicit function of Y in terms of X and 2 times the upper bound branch with the new horizontal axis would give the answer.
EDIT-the integral is solvable,it needs calculations and now I got the answer 1735.
Log in to reply
Yes, you can do it this way, but the computations are quite tedious.
What r u studying now and when we ll get all these in maths
Log in to reply
I had done a normal jee prep and started using the concepts...mathematics is the subject which I love the most
Nice sir!!! We've got similar solutions.. This is a very nice problem.
We can also solve this problem by converting the equation x 3 + y 3 = 3 a x y into polar coordinates. So we get r = cos 3 θ + sin 3 θ 3 a sin θ cos θ . Dividing both the numerator and denominator by cos 3 θ we obtain that r = 1 + tan 3 θ 3 a sec θ tan θ . Now the given area can be expressed as A = 2 1 ∫ 0 π / 2 r 2 d θ = 2 1 ∫ 0 π / 2 ( 1 + tan 3 θ ) 2 9 a 2 sec 2 θ tan 2 θ d θ = 6 9 a 2 ∫ 0 π / 2 ( 1 + tan 3 θ ) 2 d tan 3 θ = − 2 3 a 2 1 + tan 3 θ 1 ∣ ∣ ∣ ∣ 0 π / 2 = 2 3 a 2 . In this case a = 3 1 7 2 9 , so the area A = 6 1 7 2 9 2 , and, therefore, the answer is 1 7 3 5 .
You can also get the solution by usage of the formula for the cubic equation in y. This brings y 1 ( x ) , y 2 ( x ) , i.e. the two curves including the area wanted. After determination of maximum x to 914.872 by setting y 1 ( x ) = y 2 ( x ) you have the integration range to numerically calculate the integral of the area v between the two curves delivering v = 498240.1666 => 6 v = 1 7 2 9 2 .
This is a Folium of Descartes , x 3 + y 3 = 3 a x y , with a = 3 1 7 2 9 . The loop C of this curve (i.e., the part in the first quadrant) can be parametrized by x = 1 + t 3 3 a t , y = 1 + t 3 3 a t 2 for t ≥ 0 . Thus the area enclosed by C is ∫ C x d y = − 9 a 2 ∫ 0 ∞ ( 1 + t 3 ) 3 t 2 ( t 3 − 2 ) d t = − 9 a 2 [ 6 ( 1 + t 3 ) 2 1 − 2 t 3 ] 0 ∞ = 2 3 a 2 = 6 1 7 2 9 2
The sum we seek is 1 7 3 5