I find money in the jar
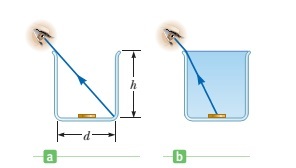 A person looking into an empty container is able to see the far edge of the container’s bottom. The height of the container is
, and its width is
. When the container is completely filled with a fluid of index of refraction
and viewed from the same angle, the person can see the center of a coin at the middle of the container’s bottom.
A person looking into an empty container is able to see the far edge of the container’s bottom. The height of the container is
, and its width is
. When the container is completely filled with a fluid of index of refraction
and viewed from the same angle, the person can see the center of a coin at the middle of the container’s bottom.
Question is that if the the container has a width of and is filled with water, then find the height of the container in to 2 decimal places.
Details and assumptions
- The refractive index, for water is .
- Use calculator if required.
The answer is 4.73.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
To solve the problem, we use Snell's law which states:
s i n θ 2 s i n θ 1 = n 1 n 2
where, θ 1 and θ 2 are angle of incident and refraction (with normal), and n 1 and n 2 , the refractive indices of the two media respectively.
Now, s i n θ 1 = h 2 + 8 2 8 , s i n θ 2 = h 2 + 4 2 4 , n 1 = n a i r = 1 , and n 2 = n = 1 . 3 3 3 .
Therefore, s i n θ 2 s i n θ 1 = n 1 n 2
⇒ h 2 + 8 2 8 × 4 h 2 + 4 2 = 1 1 . 3 3 3 ⇒ h 2 + 6 4 2 h 2 + 1 6 = 1 . 3 3 3 ⇒ 4 ( h 2 + 1 6 ) = 1 . 3 3 3 2 ( h 2 + 6 4 ) ⇒ 2 . 2 2 h 2 = 4 9 . 7 2 0 8 9 6 ⇒ h 2 = 2 2 . 3 6 5 4 5 8 1 4 ⇒ h = 4 . 7 2 9 2 1 3 2 6 8 ≈ 4 . 7 3 c m