I found an interesting geometry question

Geometry Level 3

This is not an original problem.

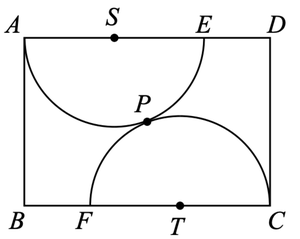
Rectangle $ABCD$ , with side lengths $AB=4$ and $BC=6$ , inscribes two identical semicircles with centers $S$ and $T$ . The two semicircles touch at point $P$ . Find the radius of the semicircle.

The answer is 2.167.

2 solutions

Krishna Karthik
Oct 19, 2020

I have drawn the desirable right-angled triangle which will relate the radii to the information given.

Basically, the hypotenuse will conveniently be $2r$ , the adjacent (with respect to $\angle FTC$ ) will be $4$ , and the opposite will be $6-2r$ , if you take away the radii from the length of the triangle.

The equation:

$(2r)^2 = 4^2 + (6-2r)^2$

Solving this will get you $\displaystyle r = \boxed{\frac{52}{24}}$

@Krishna Karthik , you have to mention that the two semicircle has the same radius.

Chew-Seong Cheong - 7 months, 3 weeks ago

Ah; sorry. I forgot about that. Now the problem's edited.

Krishna Karthik - 7 months, 3 weeks ago

I have edited the figure and the problem statement for you.

Chew-Seong Cheong - 7 months, 3 weeks ago

Right. Thanks mate.

Krishna Karthik - 7 months, 3 weeks ago

Ron Gallagher
Oct 20, 2020

Choose a coordinate system that puts B at (0,0). Then, if R is the radius, T has coordinates (6-R,0) and S has coordinates (R,4). The square of the distance between S and T is then (6-2 R)^2 +16. However, the distance between S and T is also 2 R, so that the square of the distance between S and T is also 4*R^2. Setting these two expressions equal and solving for R yields R = 13/6.

I found an interesting geometry question

The answer is 2.167.

2 solutions

0 pending reports