I have discovered a truly marvelous demonstration of this proposition, but

Number Theory Level 3

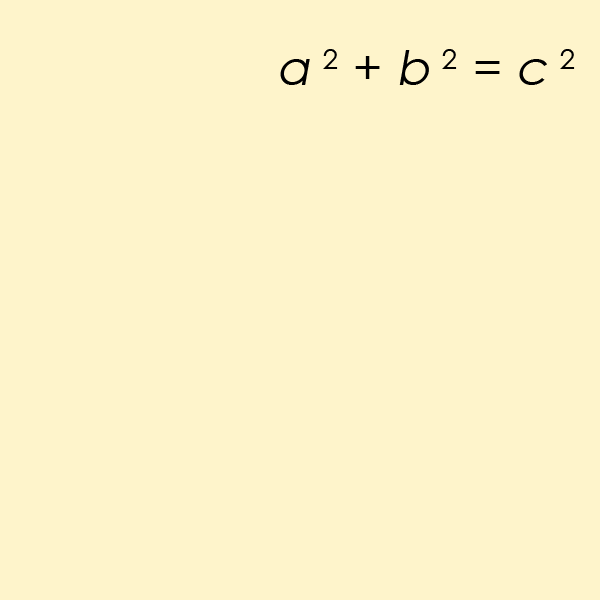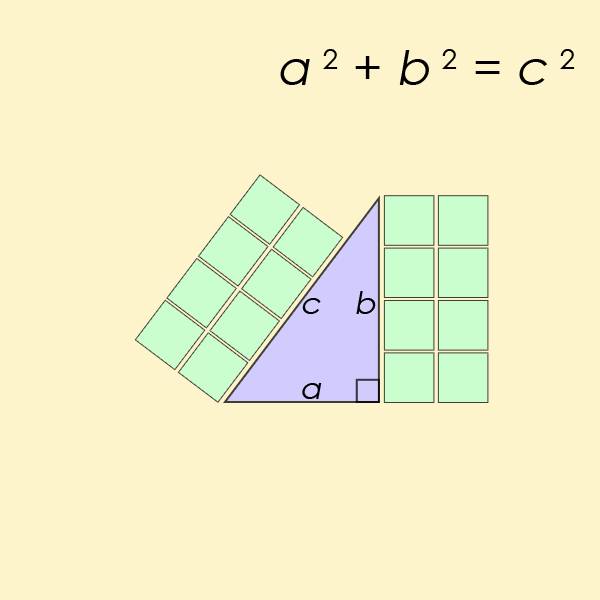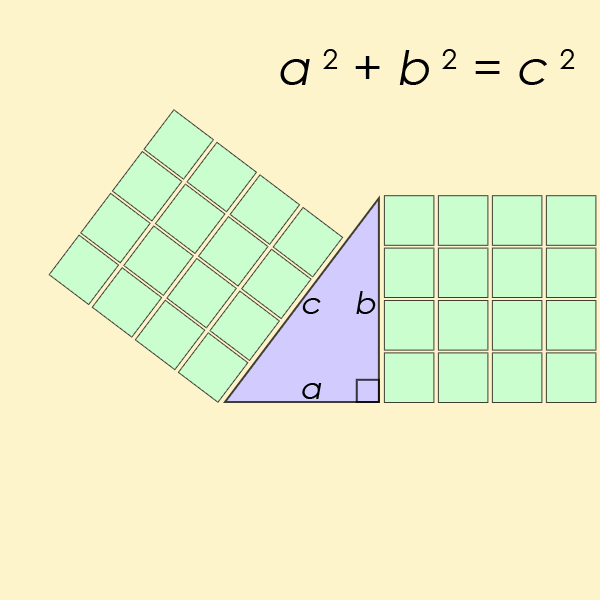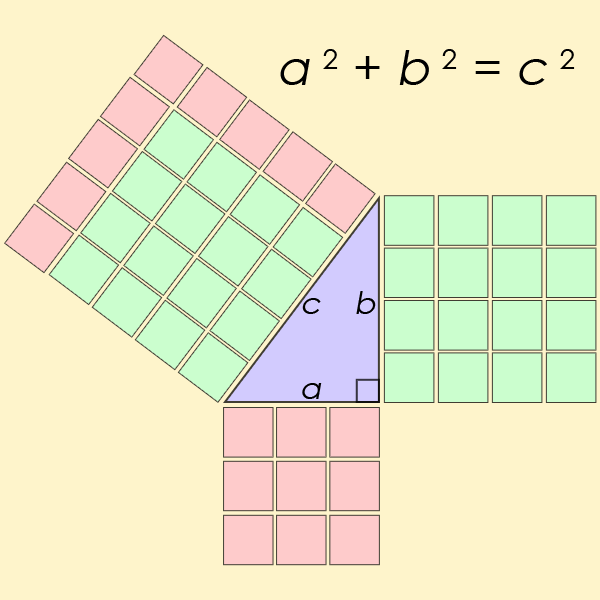$\large \displaystyle x^z + y^z = 5^z$

If $x,y,z$ are integers, find the total number of triplets $(x,y,z)$ that satisfy the equation above.

Image Credit: Wikimedia AmericanXplorer13 .

8 16 4 Countably infinite 2

5 solutions

Josh Banister
May 23, 2015

Let $z = 1$ since z can be any integer. The equation now becomes $x + y = 5$ . If we have a solution $(x, y)$ then we can also have another unique solution $(x+1, y-1)$ . Since $(0, 5)$ is a solution then by induction we have infinite solutions for $(x, y, z)$ It all comes down the domain of the variable which is only limited to the integers and nothing more.

Moderator note:

Yes correct. Bonus question: If we add the constraint that $x,y \ne 0$ and $z \ne 1$ , is it still true that the answer is countably infinite?

Bonus question answer: no there would be only 2 solutions

Mrigank Krishan - 6 years ago

No, it's more than two: $(3,4,2),(3,-4,2),(-3,-4,2),(-3,4,2),(4,3,2), \ldots$ .

But is still finite.

You also need to prove that $\frac1{x^2} + \frac1{y^2} = \frac1{25}$ has no integer solution.

Pi Han Goh - 6 years ago

The example that you gave was a triangle. A triangle cannot have sides with negative lengths. The diagram was very misleading.

Michael Horton - 6 years ago

no then also it will be countably infinite,because any 0^x + 5^x = 5^x

Atanu Roy - 6 years ago

Charles Dutertre
May 23, 2015

Well, take $x=0,y=5$ and then the equation holds for any $z \in \mathbb{N}^*$ . This should probably not be level 3.

Moderator note:

Yes correct. Bonus question: Can you decipher what the title of this problem means?

Title: "I have discovered a truly marvelous demonstration of this proposition, but"

this puzzled me already when I started then problem... This with the gif which seems quite irrelevant ... But probably is not? Or just a false indication for solving the problem maybe. No I don't see! I don't even know if you mean pythagore or $x^z+y^z = 5^z$ Arrrg no I need a hint !!

Charles Dutertre - 6 years ago

The meaning of the title is more historical than mathematical. It hints to the Fermat's Last Theorem . This was the original quote by Fermat:

" It is impossible to separate a cube into two cubes, or a fourth power into two fourth powers, or in general, any power higher than the second, into two like powers. I have discovered a truly marvellous proof of this, which this margin is too narrow to contain. "

Prasun Biswas - 6 years ago

Reynan Henry
May 23, 2015

If z is negatif we can find infinite solution

Moderator note:

Even if that is true, you failed to explain why you would get infinite number of solutions.

Where's your proof?

Pi Han Goh - 6 years ago

Chandrachur Banerjee
May 23, 2015

take z=1, then x+y=5. Now take any integer x. 5-x is an integer. So every integer can give a solution.. No other option matches. Actually are -ve z also 2 be considered??

Moderator note:

Yes. It clearly said that $x,y,z$ are integers, it did not explicit say that they are positive or negative, so you must consider both scenarios. And of course the value $0$ .

Read the question again.

Pi Han Goh - 6 years ago

Mark Macqueen
May 27, 2015

Every square number is the sum of odd numbers ∑(2n+1). So each successive number of square numbers is and integer odd number from each other. This results in a countably infinite number of equations.

Moderator note:

Wrong. Your logic is flawed. "So each successive number of square numbers is and integer odd number from each other." made no connection to the problem. And there is only a finite number of solutions when $z=2$ .

So you're saying that you can find infinite number of solutions with $z=2$ ? If so, name me 13 such solutions.

Pi Han Goh - 6 years ago

Two successive square numbers are an odd number apart. As there is an infinite number of square numbers, there is also an infinite number of odd numbers that fulfil the criteria.

Mark Macqueen - 6 years ago

If you say that's true, then just name me 13 solutions, it should be a simple task since you said that there's infinite number of solutions.

Pi Han Goh - 6 years ago

at n=2, it becomes x^2+y^2=25.

that's circle eq. so, only 8 integer sol.

variations of (3,4) and (0,5)

Tom Clancy - 5 years, 12 months ago

I have discovered a truly marvelous demonstration of this proposition, but

Image Credit: Wikimedia AmericanXplorer13 .

5 solutions

Moderator note:

Moderator note:

Moderator note:

Moderator note:

Moderator note:

0 pending reports