I heart physics
You can find the symbol of love, the heart, by looking at the motion of a charged particle that's emitted from a hot wire in a specific electromagnetic field. The electric field is directed radially from the wire and has strength everywhere. The magnetic field is parallel with the wire axis. If the charged particle has a very small radial velocity with absolutely no velocity parallel to the wire direction when it escapes the wire, find how long the total length it has to travel to come back to the wire in meters .
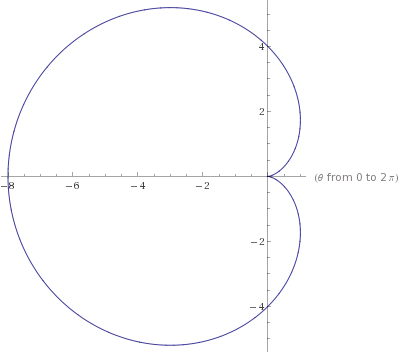
If you plot the orbit of the particle you'll find that it looks like a heart!
Details and assumptions
- Neglect the size of the wire.
- The electric charge of the particle is and the mass is (just to simplify the calculations for this problem).
The answer is 32.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The equation of motion for the electron in the polar coordinate around the wire is:
m ( 2 r ˙ θ ˙ + r θ ¨ ) = m r d t d ( r 2 θ ˙ ) = e B r ˙ = e B d t d r ⇒ m d t d ( r 2 θ ˙ ) = e B r ˙ = e B 2 d t d ( r 2 )
⇒ m r 2 θ ˙ = 2 e B r 2 ⇒ θ ˙ = 2 m e B = ω
m ( r ¨ − r θ ˙ 2 ) = e E − e B r θ ˙ ⇒ r ¨ + 4 m 2 e 2 B 2 r = r ¨ + ω 2 r = e E ⇒ r ( t ) = e B 2 4 m 2 E − R c o s ( ω t + ϕ )
Using the boundary condition r ( t = 0 ) = 0 and r ˙ ( t = 0 ) = v ≈ 0 we get ϕ = 0 and R = e B 2 4 m 2 E :
r = e B 2 4 m 2 E ( 1 − cos ( ω t ) ) = e B 2 4 m 2 E ( 1 − cos θ )
The orbit looks like a heart!
The total length is pretty easy to calculate:
s = ∫ 0 2 π ( d r 2 + r 2 d θ 2 ) 1 / 2 = ∫ 0 2 π e B 2 4 m 2 E 2 + 2 cos θ d θ = e B 3 2 m 2 E = 3 2 ( m )