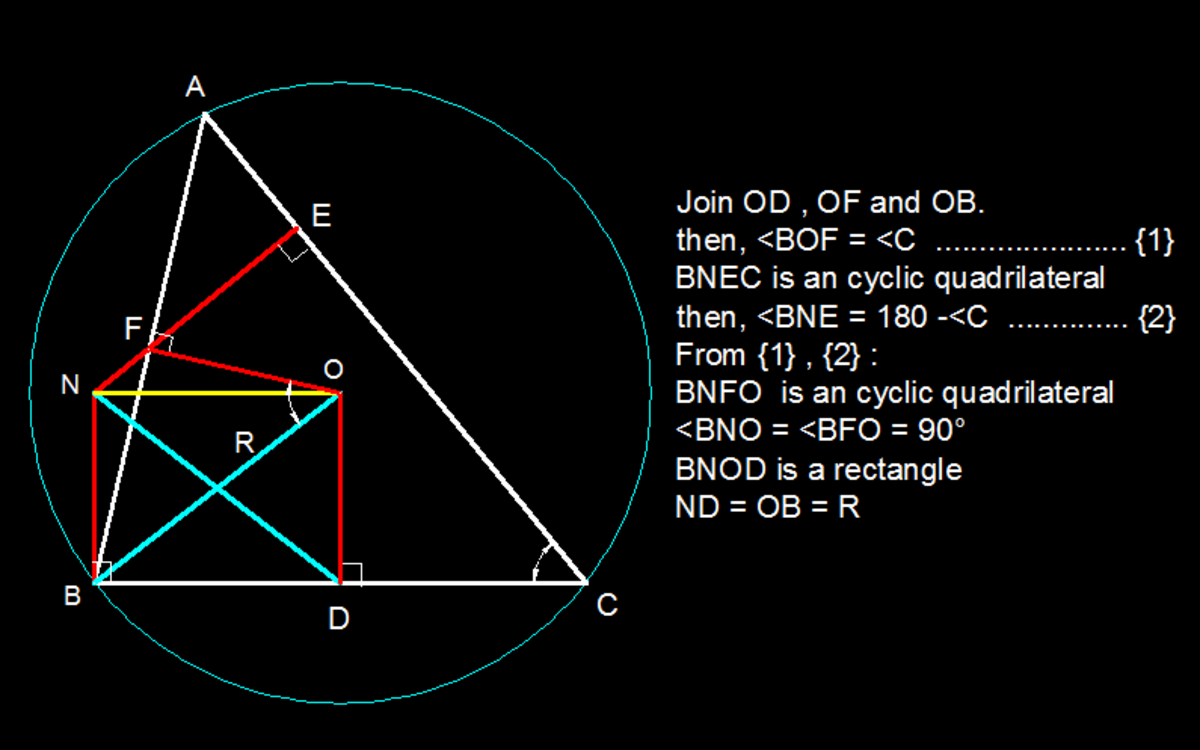
A geometry problem by Vishwash Kumar ΓΞΩ

Let the circumcentre $O$ of the triangle be the origin for a system of vectors. Then $\overrightarrow{OA} \; = \; \mathbf{a} \hspace{1cm} \overrightarrow{OB} \; = \; \mathbf{b} \hspace{1cm} \overrightarrow{OC} \; = \; \mathbf{c}$ where $|\mathbf{a}| = |\mathbf{b}| = |\mathbf{c}| = R$ , the circumradius. Consider the point $N$ with position vector $\overrightarrow{ON} = \tfrac12(\mathbf{b}-\mathbf{c}) = \tfrac12\overrightarrow{CB} = \overrightarrow{DB}$ . Then, since $\overrightarrow{OD} = \tfrac12(\mathbf{b}+\mathbf{c})$ , we see that $\overrightarrow{ON} \cdot \overrightarrow{OD} = 0$ .

Now $\overrightarrow{NB} = \tfrac12(\mathbf{b}+\mathbf{c}) = \overrightarrow{OD}$ , so that $N$ lies on the line through $B$ perpendicular to $BC$ . Moreover $\overrightarrow{NF} = \tfrac12(\mathbf{a}+\mathbf{b}) - \tfrac12(\mathbf{b}-\mathbf{c}) = \tfrac12(\mathbf{a}+\mathbf{c})$ , and hence $N$ lies on the line through $F$ perpendicular to $AC$ . Thus $N$ is the point described in the question.

It is clear from the above that $ONBD$ is a rectangle, and hence its diagonals are equal. Thus $ND = OB = R$ , making the desired ratio equal to $\boxed{1}$ .