Number Of Digits Corresponds to Logarithm?
Find the number of digits in 6 1 2 0 .
Use the approximations lo g 2 = 0 . 3 0 1 0 and lo g 3 = 0 . 4 7 7 1 .
The answer is 94.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
The ceiling function does not always work. It should be the floor function +1.
Log in to reply
Great observation! When does the ceiling function fail to work?
Log in to reply
It won't work when you are finding the length of numbers of form 1 0 x
@Akshat Sharda dats cool!!!!
U gave wrong info Instead of giving the value of log2 and log 3 u can give directly value of log6
That would be might easy
Log in to reply
well the information is not wrong, its more of they wanted to add the use of log laws into the problems
The point of the question is to determine the value of log 6, from log 2 and log 3.
Review logarithms .
Same way :v
120 log 2 = 36.12
120 log 3 = 52.25
120(log 2 + log 3) = 93.37
120(log 6)=93.37
log 6^120 = 93.37
10^93.37 = 6^120
therefore there are 94 digits
( l o g 2 ) + ( l o g 3 ) = l o g ( 2 × 3 ) = l o g ( 6 ) = 0 . 3 0 1 0 + 0 . 4 7 7 1 = 0 . 7 7 8 1
6 1 2 0 = 6 1 0 0 + 1 0 + 1 0 = 6 1 0 0 × 6 1 0 × 6 1 0
0 . 7 7 8 1 1 0 0 + 2 × ( 0 . 7 7 8 1 1 0 ) = 9 3 . 3 7 2 ≈ 9 4
This can be done without the values given by knowing a couple of useful pure power coincidences.
Clearly 6 1 2 0 = 2 1 2 0 ⋅ 3 1 2 0 .
The first coincidence to use is 3 1 2 ≈ 2 1 9 . Therefore 3 1 2 0 ≈ 2 1 9 0 .
Using the exponent rules we now have 6 1 2 0 ≈ 2 3 1 0 .
The second coincidence to use is 2 1 0 ≈ 1 0 3 . Therefore 2 3 1 0 ≈ 1 0 9 3 .
Knowing the second approximation slightly reduced the quantity, and that the error of the first approximation is smaller than the error of the second, we have confidence that 6 1 2 0 > 1 0 9 3 therefore the true quantity will have 94 digits.
Moderator note:
This approach, while correct, is unnecessarily complicated.
It also looks like you used a calculator to evaluate the expression, as opposed to only using the information that was given.
A very general way to do these type of question is
If we want to find the number of digits in a b
Simply we can do
[b (log a)] + 1
Or if b(log a) is in decimals just round it off to the next integer without adding 1
Moderator note:
That's the general approach. How does it apply to this specific problem?
From the formula
[120 (log 6)]
[120 ( 0.7781)]
=93.3781
We can just round it of to the next integer
which is 94
Log in to reply
Great
Note that it's not "round if off to the next integer", but should be "round it down to the next integer and add 1".
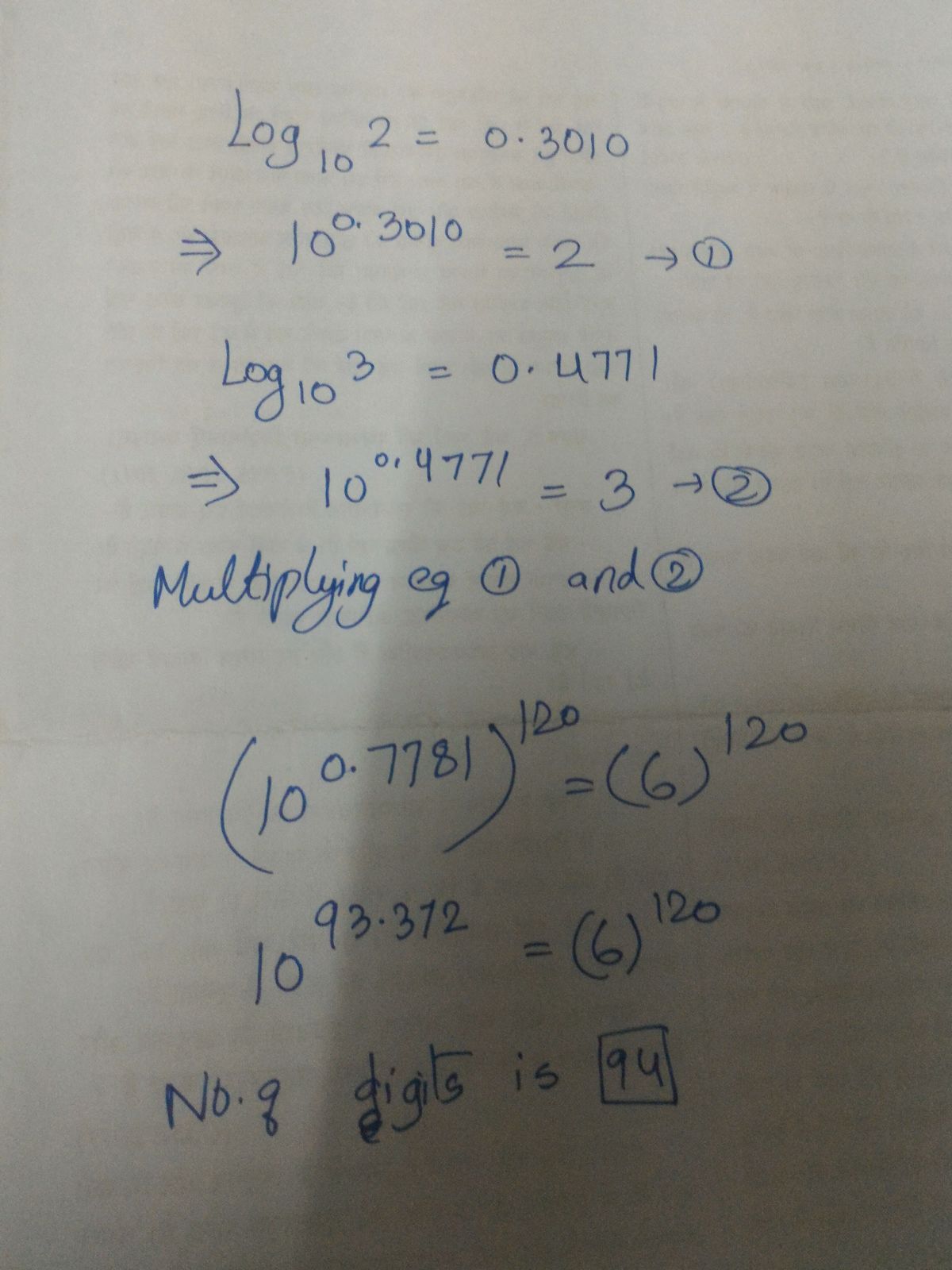

A direct way to do these type of questions,
⌊ lo g 6 1 2 0 ⌋ + 1 = ⌊ 1 2 0 lo g 6 ⌋ + 1 ⌊ 1 2 0 ( lo g 2 + lo g 3 ) ⌋ + 1 = ⌊ 1 2 0 ( 0 . 7 7 8 1 ) ⌋ + 1 ⌊ 9 3 . 3 7 2 ⌋ + 1 = 9 4