I love being inspired! 8
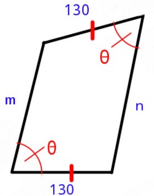
In the above quadrilateral, m = n and perimeter of the figure is 500 units.
Find the value of ⌊ 1 0 0 0 cos θ ⌋ .
The answer is 923.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
exact same method!
I hope my image comes in ok. I took a visual approach.
Let p be the diagonal through the vertices containing the unequal angles. From the top triangle, applying Cos Rule, p 2 = 1 3 0 2 + n 2 − 2 6 0 ∗ n ∗ C o s θ . From the bottom triangle, applying Cos Rule, p 2 = 1 3 0 2 + m 2 − 2 6 0 ∗ m ∗ C o s θ . ∴ m 2 − n 2 = 2 6 0 ∗ ( m − n ) ∗ C o s θ . B u t m = n . A n d m + n = 5 0 0 − 2 6 0 = 2 4 0 . ⟹ C o s θ = 1 3 1 2 . ∴ ⌊ 1 0 0 0 ∗ C o s θ ⌋ = 9 2 3 .
This is hardly any different from the solution of Aditya Agarwal .
We have m + n = 5 0 0 − 2 6 0 = 2 4 0 By the cosine rule on dividing the quadrilateral into two triangles whose two sides are ( 1 3 0 , n ) and ( 1 3 0 , m ) , and a common side, we have 1 3 0 2 + m 2 − 2 6 0 m cos θ = 1 3 0 2 + n 2 − 2 6 0 n cos θ m + n = 2 6 0 cos θ = 2 4 0 So we get cos θ = 1 3 1 2 So ⌊ 1 3 1 2 ∗ 1 0 0 0 ⌋ = 9 2 3