I love being Inspired! (Part-3)

Logic Level 3

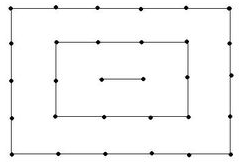
Two logicians Anshuman and Akshat were playing 'Dots and Boxes'.

The rules of the game is as follows:

Players take turns alternatively joining two horizontally or vertically adjacent dots by a line.
A player that completes the fourth side of a square (a box) colours that box and must play once again, without passing it to the other.
When all the boxes have been colored, the game ends and the player who has coloured more boxes wins.

In the given image, if its Akshat's turn to draw a line, then who among them will win this game if both play optimally?

Akshat Anshuman Anyone can Cannot be determined

2 solutions

Akshat Sharda
Sep 27, 2015

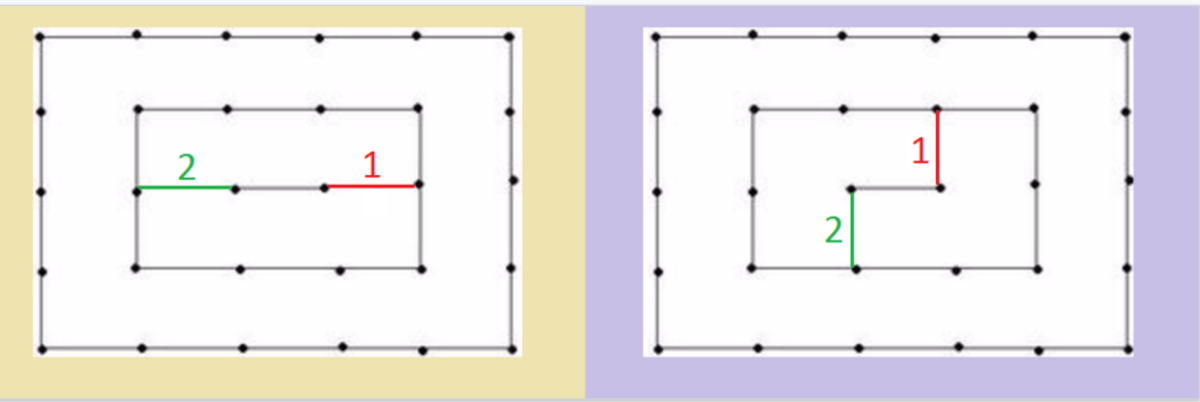
Solution : Now as its Akshat's turn (my turn!) he will try to win and he will join Any two dots in the smaller rectangle and then all the boxes within the smaller rectangle $(6)$ will be of coloured by Anshuman (playing according to the rules) and then Anshuman have to join Any two dots in the bigger rectangle and then Akshat will be having all the boxes $(14)$ and thus Akshat is likely to win.

I don't think that the first player will win. I agree that the person who finishes the smaller rectangle (and is forced to start in the bigger rectangle) will lose this game.

Because the second player can always force the first player to continue filling the smaller rectangle, the second player will win this game .

Here is the picture

Worapong Itthithaneth - 5 years, 6 months ago

If Akshat knows that he will lose in every case if he connects dots of the smaller rectangle, why would he do that? It is given that both players are logicians.

Kushagra Sahni - 5 years, 5 months ago

I think you are correct and the second player is the one who would actually win the game if both are clever enough to figure it out.

Jerry Hill - 5 years, 4 months ago

I lost it..... Huhhh...😠😠😠😠 But if you would have joined the dots of bigger rectangle, I would have won it..

Anshuman Singh Bais - 5 years, 8 months ago

Jerry Hill
Jan 18, 2016

Solution to the updated question. "In the given image, if its Akshat's turn to draw a line, then who among them will win this game if both play optimally?"

Anshuman

The game is in such a position that the first person to connect 2 dots in the outer box first would win the game. This is because the second player then would be able to fill out all the boxes in the outer square.

Move 1: Akshat would join 2 dots in the inner square.

Move 2: Anshuman will not join 2 dots in the outer square because it will make him lose. Anshuman will not fill the square that Akshat started because he will have to draw the line in the outer square which would make him lose. So his optical move would be to join another line in the inner square that will not make a square. (see image below)

Move 3. Whichever move Akshat makes, he will join 2 dots in the outer square

Move 4 which leaves all those squares for Anshuman to fill up.

Winner : Anshuman.

Solution to the question before: "In the given image, if its Akshat's turn to draw a line, then who among them can win this game?" Anyone can

Credits for image: Worapong Itthithaneth

Anshuman can force Akshat to start a line on the outer square.

It implies that, if both players play optimally, Anshuman would win.

But the question is, then who among them can win this game?

Since both can win the game, the answer should be Anyone can.

I love being Inspired! (Part-3)

2 solutions

0 pending reports