I love parallelograms. How about you? - Correct version
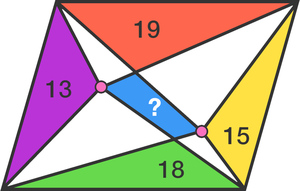
I place 2 points (in pink) inside a parallelogram, and then draw a line segment from each point to each of the 4 vertices of this parallelogram, dividing it into 9 parts.
If the four triangles in the diagram have areas 13, 15, 18, and 19, respectively, what is the area of the blue quadrilateral?
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
In my solution the two points are F and H .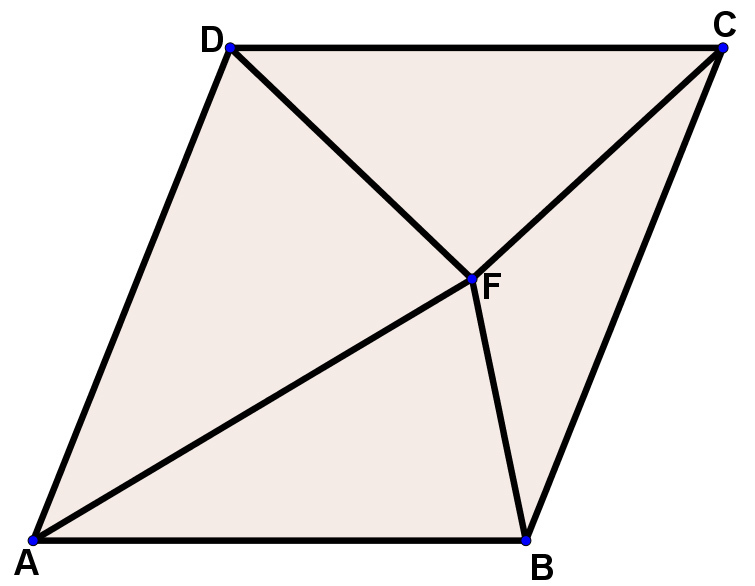
If we draw parallel to the parallelogram's sides through H, we make four parallelograms, and since a diagonal divides a parallelogram to two equal parts,
[
A
B
H
]
+
[
C
D
H
]
=
[
B
C
H
]
+
[
A
D
H
]
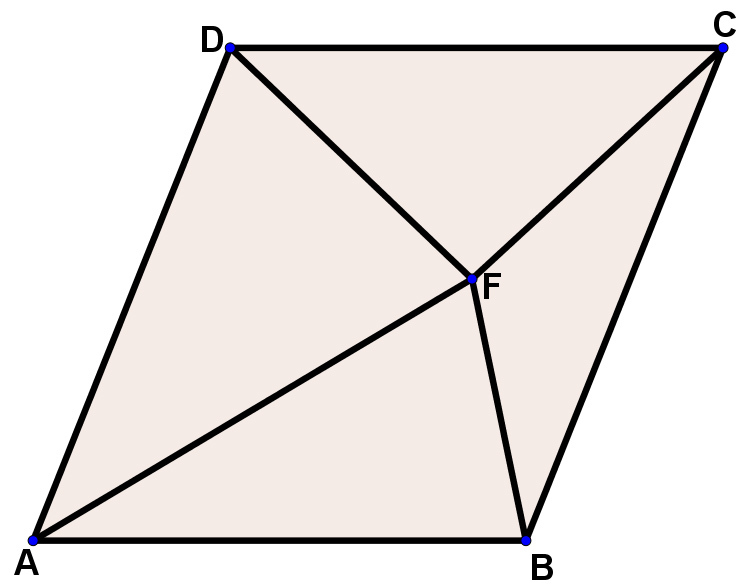Similarly,
[
A
B
F
]
+
[
C
D
F
]
=
[
B
C
F
]
+
[
A
D
F
]
From this two equation we get
[
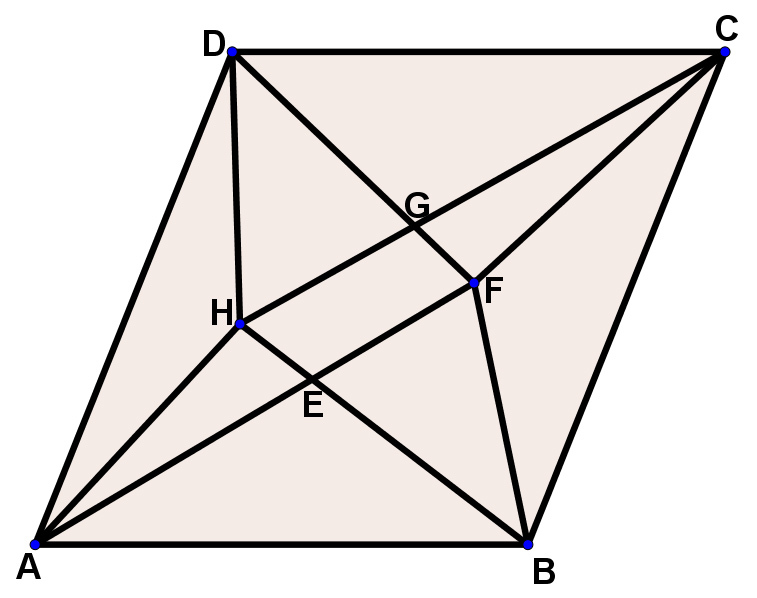A
H
D
]
+
[
A
F
D
]
+
[
B
F
C
]
+
[
B
H
C
]
−
(
[
A
E
H
]
+
[
G
D
H
]
+
[
B
E
F
]
+
[
F
C
G
]
)
=
[
A
B
H
]
+
[
C
D
H
]
+
[
A
B
F
]
+
[
C
D
F
]
−
(
[
A
E
H
]
+
[
G
D
H
]
+
[
B
E
F
]
+
[
F
C
G
]
)
⇒
[
A
H
D
]
+
[
B
F
C
]
+
[
E
F
G
H
]
=
[
A
B
E
]
+
[
C
D
G
]
⇒
[
E
F
G
H
]
=
[
A
B
E
]
+
[
C
D
G
]
−
(
[
B
F
C
]
+
[
A
H
D
]
)
⇒
[
blue quadrilateral
]
=
[
green triangle
]
+
[
red triangle
]
−
(
[
yellow triangle
]
+
[
purple triangle
]
)
=
3
7
−
2
8
=
9