I need more!
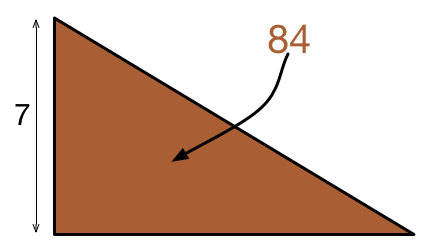 A right triangle has a leg of length
7
m
and an area of
8
4
m
2
. What is its perimeter?
A right triangle has a leg of length
7
m
and an area of
8
4
m
2
. What is its perimeter?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
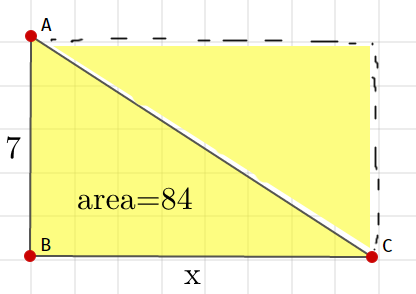
From the picture, we can say
7 x = 8 4 × 2
x = 2 4
Using Pythagoras
7 2 + 2 4 2 = 4 9 + 5 7 6 = 6 2 5
H y p o t e n e u s e = 6 2 5 = 2 5
Therefore the perimeter is 7 + 2 4 + 2 5 = 5 6
Nice image!
Write a solution. Area = x*7/2=84 where x=length of other leg. x=24; hypotenuse=(7^2+24^2)^(1/2) = 625^(1/2) = 25. Perimeter=7+24+25 = 56.
Because the area of the triangle is 84 units, 74=1/2bh. bh=168. 7b=168 b=24. From the basic Pythagorean triple 7+24+25 one gets 56 units as the perimeter.
Right! I think it will be slightly harder to be given a side length and a perimeter, and then find the area.
Though, with any "integer triangle", that reduces the possibilities and makes the problems much easier.
let b be the base and h be the hypotenuse of the right triangle
The area of a triangle is given by, A = 2 1 × b a s e × h e i g h t .
Substitute the given values,
8 4 = 2 1 ( b ) ( 7 )
b = 2 4
Applying pythagorean theorem,
h = 7 2 + 2 4 2 = 6 2 5 = 2 5
Therefore,
P = 2 4 + 7 + 2 5 = 5 6 m
84= 1/2 b 7 84*2/7=b b=24. using pythagoras theorem: h^2=7^2 +24^2 h^2=625 h=25 perimeter= sum of all sides. ie 7+24+25=56
(1/2) * 7x = 84 7x = 2 * 84 7x = 168 x = 168/7 = 24 by Pythagoras 7^2+ 24^2 = H^2 H = 625 ^ (1/2) H = 25 perimeter = 24+25+7 = 56
Using the formula of area of right triangle, we can find the length of the other
side of the right angle to be 24
Using the Pythagoras theorem, we can find the length of the hypotenuse to be 25
So the perimeter = 7 + 24 + 25 = 56
The area of the triangle is given by the formula: A = 2 1 b h where b = base and h = height
Substituting, we get
8 4 = 2 1 ( 7 ) ( b ) ⟹ b = 2 4
By pythagorean theorem, we have
c 2 = 7 2 + 2 4 2 ⟹ c 2 = 6 2 5 ⟹ c = 6 2 5 ⟹ c = 2 5
Finally the perimeter is
P = 7 + 2 4 + 2 5 = 5 6 m