I need my 5 \sqrt5 index

Geometry Level 4

Find the area of a cyclic pentagon with circumradius 85 and lengths 72, 80, 26, 154, and 136.


The answer is 13104.

Sal Gard by Sal Gard , 19, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Ahmad Saad
Jul 8, 2016

2 Helpful 0 Interesting 0 Brilliant 0 Confused

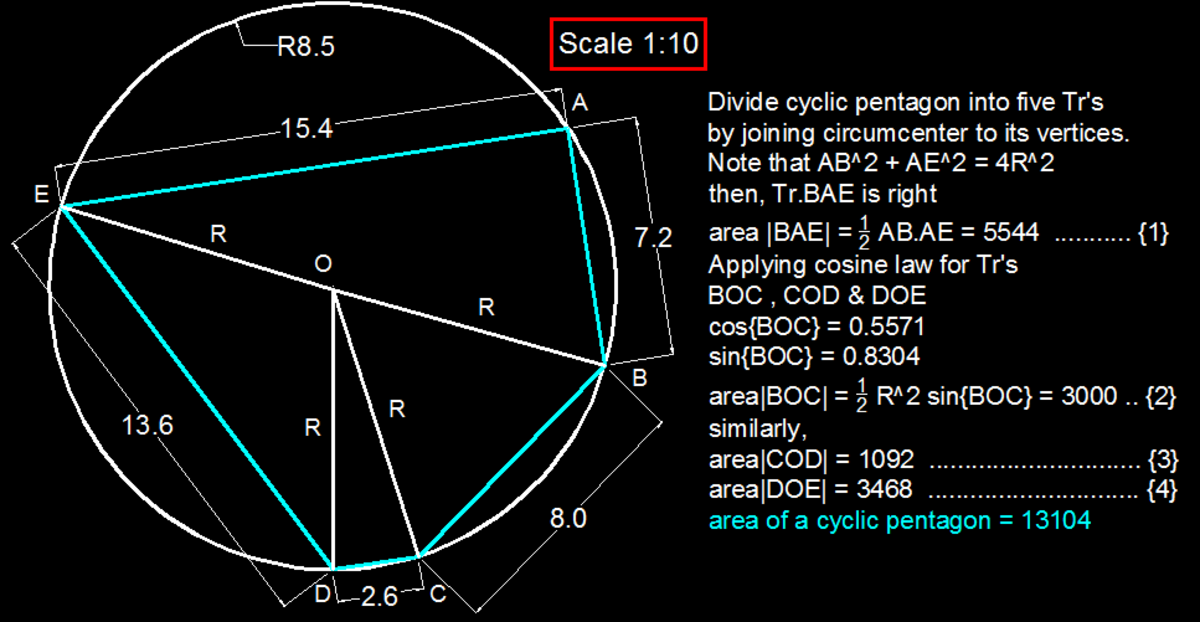
Great thanks for the solution. I like this new approach. I will be posting a sequel.

Sal Gard - 4 years, 11 months ago
Ujjwal Rane
Jul 25, 2016

@Sal Gard This is an amazing pentagon! How did you ever find this? Fascinating find!

The area is the sum of five isosceles triangles. And all have not only integer sides but also integer altitudes!!

Area = 8 5 2 − 3 6 2 × 36 + 8 5 2 − 4 0 2 × 40 + 8 5 2 − 1 3 2 × 13 + 8 5 2 − 7 7 2 × 77 + 8 5 2 − 6 8 2 × 68 \sqrt{85^2-36^2} \times 36 + \sqrt{85^2-40^2} \times 40 + \sqrt{85^2-13^2} \times 13 + \sqrt{85^2-77^2} \times 77 + \sqrt{85^2-68^2} \times 68

= 77 × 36 + 75 × 40 + 84 × 13 + 36 × 77 + 51 × 68 = 13104 77 \times 36 + 75 \times 40 + 84 \times 13 + 36 \times 77 + 51 \times 68 = \textbf{13104}

0 Helpful 0 Interesting 0 Brilliant 0 Confused

These pentagons are known as Robbins' pentagons. They can be generated through multivariable equations. A lot of open questions exist in this area. I just put a basic problem. Glad you liked it.

Sal Gard - 4 years, 10 months ago

Log in to reply

Thanks for the pointer, I will look it up!

Ujjwal Rane - 4 years, 10 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...