I Need No Corners (Count 'em All 13!)
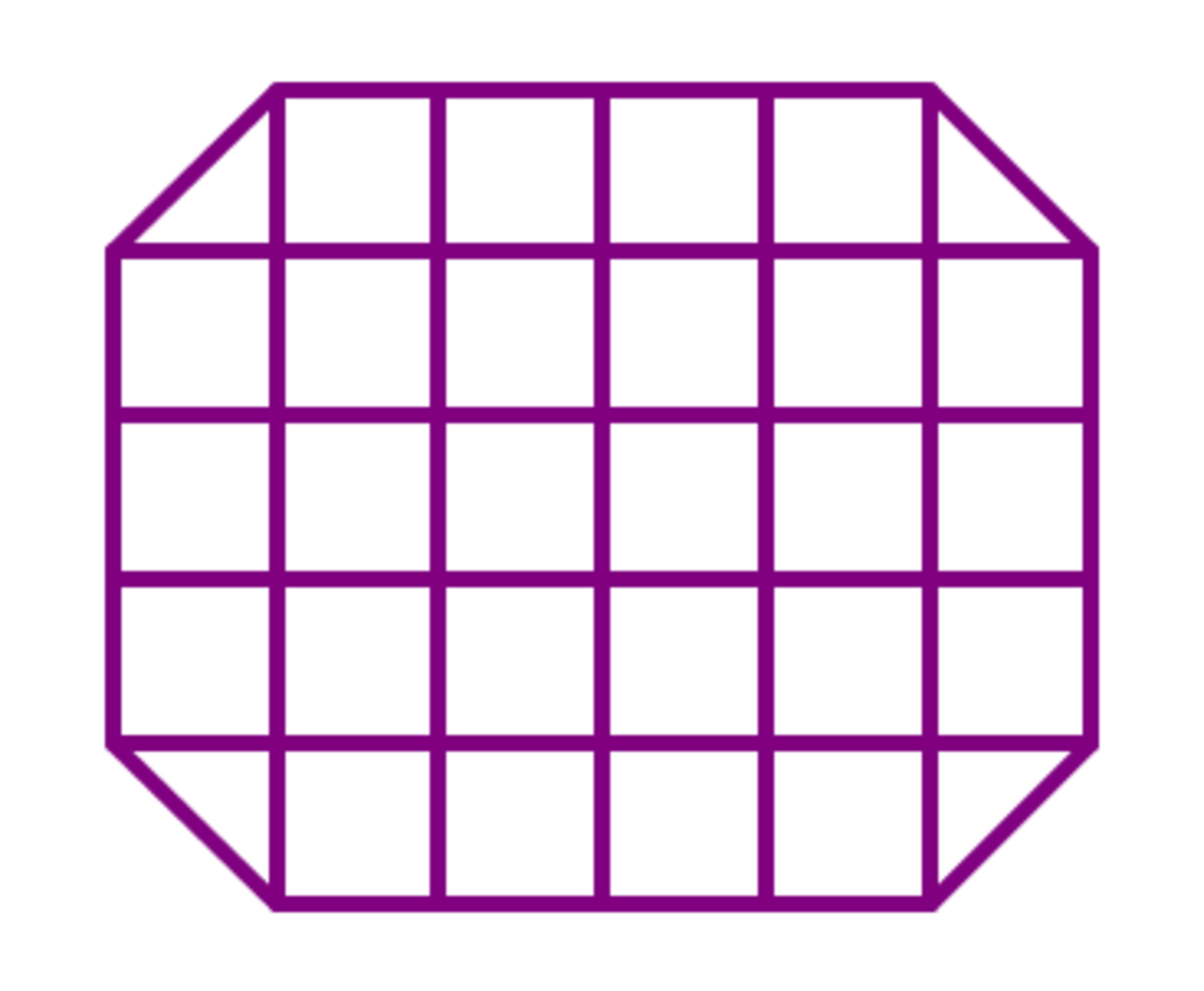
The figure above shows a 6 × 5 grid but this time with all 4 corners cut off forming triangles.
Count the total number of quadrilaterals in the grid above.
Clarification :
- A quadrilateral is a polygon that has 4 sides.
This is one part of Quadrilatorics .
The answer is 248.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
You could have simply implied inclusion-exclusion.

Careful counting shows that the above figure with
6
columns and
1
row has
6
+
5
+
4
+
3
+
2
+
1
=
2
1
quadrilaterals.

Careful counting shows that the above figure with
6
columns and
2
rows has
1
2
+
1
0
+
8
+
6
+
4
+
2
+
6
+
5
+
4
+
3
+
2
+
1
=
6
3
quadrilaterals.

Careful counting shows that the above figure with
6
columns and
3
rows has
1
8
+
1
5
+
1
2
+
9
+
6
+
3
+
1
2
+
1
0
+
8
+
6
+
4
+
2
+
6
+
5
+
4
+
3
+
2
+
1
=
1
2
6
quadrilaterals.

Careful counting shows that the above figure with
6
columns and
4
rows has
2
4
+
2
0
+
1
6
+
1
2
+
8
+
4
+
1
8
+
1
5
+
1
2
+
9
+
6
+
3
+
1
2
+
1
0
+
8
+
6
+
4
+
2
+
6
+
5
+
4
+
3
+
2
+
1
=
2
1
0
quadrilaterals.
So, the figure which follows the same pattern and has
6
columns and
5
rows(i.e. the figure without the cut) should have
3
0
+
2
5
+
2
0
+
1
5
+
1
0
+
5
+
2
4
+
2
0
+
1
6
+
1
2
+
8
+
4
+
1
8
+
1
5
+
1
2
+
9
+
6
+
3
+
1
2
+
1
0
+
8
+
6
+
4
+
2
+
6
+
5
+
4
+
3
+
2
+
1
=
[
(
2
1
×
5
)
+
(
2
1
×
4
)
+
(
2
1
×
3
)
+
(
2
1
×
2
)
+
(
2
1
×
1
)
]
=
[
2
1
×
(
5
+
4
+
3
+
2
+
1
)
]
=
[
2
1
×
1
5
]
=
3
1
5
Now, it has four edges cut, so all the quadrilaterals which includes the cut part as one of its edge would not be counted. But, in this process the number of quadrilaterals which have either 1 row or 1 column would not be counted, because they become trapezium which is a quadrilateral.
Careful counting shows that there are 4 0 such quadrilaterals which have one cut part as their edge. So, yotal number of quadrilaterals with atleast one cut part as their edge = 4 × 4 0 = 1 6 0 . But we ca express one quadrilateral in two forms. For example, a ( 1 × 4 ) quadrilateral would co-incide with ( 4 × 1 ) quadrilaterals. So, all the 4 0 quadrilaterals are counted twice in rge process, so, the number of quadrilaterals which have to be excluded are 2 1 6 0 = 8 0
Now, careful counting shows that in our process we have counted 1 8 quadrilaterals which has two cut parts as their edge.
Now, again, after completing all these processes the whole figure is being counted 1 time extra. So, that too have to be excluded.
Now again, 4 cut edges form a triangle, so they have to be excluded.
So, the total number of quadrilaterals =
[
(
(
(
3
1
5
−
8
0
)
+
1
8
)
−
1
)
−
4
]
=
[
(
(
2
3
5
+
1
8
)
−
1
)
−
4
]
=
[
(
2
5
3
−
1
)
−
4
]
=
(
2
5
2
−
4
)
=
2
4
8
quadrilaterals.
□
First let's count the quadrilaterals in the sections without corners cut. We have 2 rectangles wich are 4×5 and 6×3. So the numers un quadrilaterals here are ( 2 5 ) × ( 2 6 ) and ( 2 7 ) × ( 2 4 ) . Now there is a central part which was conted twice so remove that. It is 4×3 so ( 2 5 ) × ( 2 4 ) . Now the last things are the quadrilaterals with a corner cut. They can be counted from the image but I noticed that their number is the non-cut squares in the side 2 times plus 1. So for the small side they are 2 × 3 + 1 and for the long side 2 × 4 + 1 , being the sides 2 for each part these values are all taken 2 times. So ( 2 5 ) × ( 2 6 ) + ( 2 7 ) × ( 2 4 ) − ( 2 5 ) × ( 2 4 ) + 2 × ( 2 × 3 + 1 ) + 2 × ( 2 × 4 + 1 ) the result of this is 2 4 8