Count 'em Slopes (Count 'em All 17!)
A slope grid is a grid that is made by diagonally slicing a regular square grid in half. For example, the figure below shows 4 slope grids with dimensions 1 × 1 , 2 × 2 , 3 × 3 , 4 × 4 respectively.
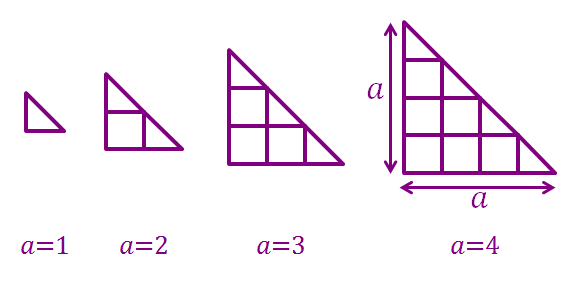
Count the total number of quadrilaterals in a 3 0 × 3 0 slope grid (that is, when a = 3 0 ).
Clarification :
- A quadrilateral is a polygon that has 4 sides.
This is one part of Quadrilatorics .
The answer is 44950.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
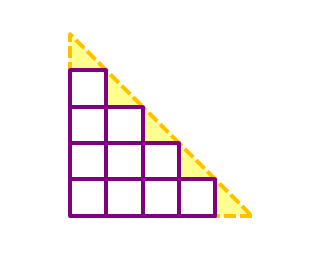
We observe that an a × a slope grid consists of an ( a − 1 ) × ( a − 1 ) staircase grid with a triangles patched along its hypotenuse.
I claim that the number of quadrilaterals in the ( a − 1 ) × ( a − 1 ) staircase grid is 2 4 a ( a − 1 ) ( a + 1 ) ( a + 2 )
I will now provide a quick sketch of the proof, you can see the full details in my solution to Count 'em Staircases (Count 'em All 16!) , if you've already seen it, you may safely skip this part. :D
Proof:
Suppose the number of quadrilaterals in an a × a staircase grid is Q a , we will try to find Q a + 1 .
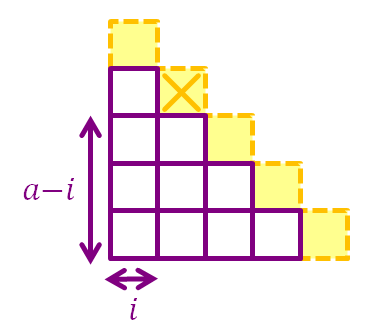
To increase a by 1, we simply add a + 1 squares to the hypotenuse (the yellow squares), the newly formed quadrilaterals must contain one of the yellow squares as its top-right corner square. If a quadrilateral's top-right corner square lies on a yellow square that is i units away from the left boundary, then it must be a − i units away from the bottom boundary, and the number of possible locations for its bottom-left corner square is ( i + 1 ) ( a − i + 1 ) .
Therefore, Q a + 1 = Q a + i = 0 ∑ a ( i + 1 ) ( a − i + 1 ) = Q a + 6 a 3 + 6 a 2 + 1 1 a + 6 .
Solving this recurrence relation with the initial condition Q 1 = 1 , we get that Q a = 2 4 a ( a + 1 ) ( a + 2 ) ( a + 3 ) .
For this problem, we want Q a − 1 , replacing a with a − 1 , we have Q a − 1 = 2 4 a ( a − 1 ) ( a + 1 ) ( a + 2 ) . □
It now remains to compute the number of trapeziums in the a × a slope grid.
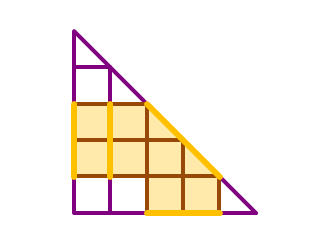
To construct a trapezium, we first need to choose a certain length of the slanted edge of the slope grid. The number of ways to choose a slanted edge of length i ( i ∈ Z + , i ⩽ a ) is a − i + 1 .
Then, we need either a matching left edge for the trapezium or a matching bottom edge for the trapezium. The total number of ways to do so with the chosen slanted edge of length i is a − i .
Therefore, the total number of trapeziums is i = 1 ∑ a ( a − i ) ( a − i + 1 )
Hmm, to make our lives slightly easier, let's make the substitution j = a − i . i iterates from 1 to a and thus j iterates from a − 1 to 0 . The above summation is therefore equivalent to j = 0 ∑ a − 1 j ( j + 1 ) . j = 0 ∑ a − 1 j ( j + 1 ) = 0 + j = 1 ∑ a − 1 j ( j + 1 ) = j = 1 ∑ a − 1 ( j 2 + j ) = 6 a ( a − 1 ) ( 2 a − 1 ) + 2 a ( a − 1 )
Hence, the number of quadrilaterals in an a × a slope grid is 2 4 a ( a − 1 ) ( a + 1 ) ( a + 2 ) + 6 a ( a − 1 ) ( 2 a − 1 ) + 2 a ( a − 1 ) = 2 4 a ( a − 1 ) [ ( a + 1 ) ( a + 2 ) + 4 ( 2 a − 1 ) + 1 2 ] = 2 4 a ( a − 1 ) ( a 2 + 3 a + 8 a + 2 − 4 + 1 2 ) = 2 4 a ( a − 1 ) ( a 2 + 1 1 a + 1 0 ) = 2 4 a ( a − 1 ) ( a + 1 ) ( a + 1 0 )
Finally, substituting a = 3 0 we would get the answer 4 4 9 5 0 .
The bottom and left sides of any quadrilateral must be horizontal and vertical. If the bottom-left vertex of a quadrilateral is chosen, then the quadrilateral is either a rectangle or else is a trapezium obtained by truncating a rectangle with the sloping line.
If the bottom-left vertex is a distance N from the sloping line, then the top-right corner of the rectangle (or the rectangle to be truncated to form the trapezium) must lie in one of the regions indicated in red in the diagram (either inside or on the triangle or else on the two line segments):
Thus there are 2 1 N ( N − 1 ) + 2 ( N − 1 ) = 2 1 ( N − 1 ) ( N + 4 ) quadrilaterals that can be formed with the chosen bottom-left vertex, and hence (since there are a + 1 − N vertices that are a horizontal distance N from the sloping line) a slope grid of size a contains a total of N = 1 ∑ a 2 1 ( N − 1 ) ( N + 4 ) × ( a + 1 − N ) = 2 4 1 a ( a 2 − 1 ) ( a + 1 0 ) rectangles. With a = 3 0 we obtain a total of 4 4 9 5 0 quadrilaterals.