I promise I won't look

Computer Science Level 4

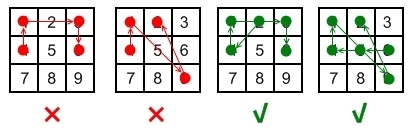
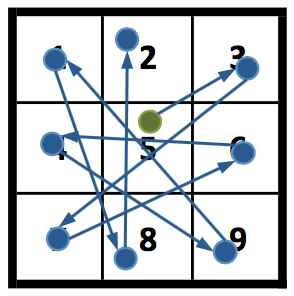
Android's lock screen feature allows people to protect their phones by joining points on a grid to make a pattern. Let $L$ be the size of the longest possible length of the pattern that can be drawn on an android phone with a $3 \times 3$ pattern lock. If the grid is spaced equally by one unit what is $L \sqrt{31}$ rounded to the nearest integer?

The rules for drawing a pattern are:

You can only use a point once
You cannot "jump" a point if it is in between the two points and is part of the line that satisfies the first two points. Ie You cannot go from 1 to 9 without also hitting 5. But you can go directly from 2 to 9 without including any other point.
ONCE a point is "taken", it may THEN be skipped. A point cannot be skipped "in transit" only if it hasn't already been taken.

To fully understand the rules, it is best to try them out on a real phone.

Details and Assumptions

The points are equally spaced vertically and horizontally by one unit.
If it had been a $2 \times 2$ grid, $L$ would be $1 + 2 \sqrt{2}$ .

Image Credits - stackoverflow, banadia.de

The answer is 99.

3 solutions

Abdelhamid Saadi
Aug 1, 2015

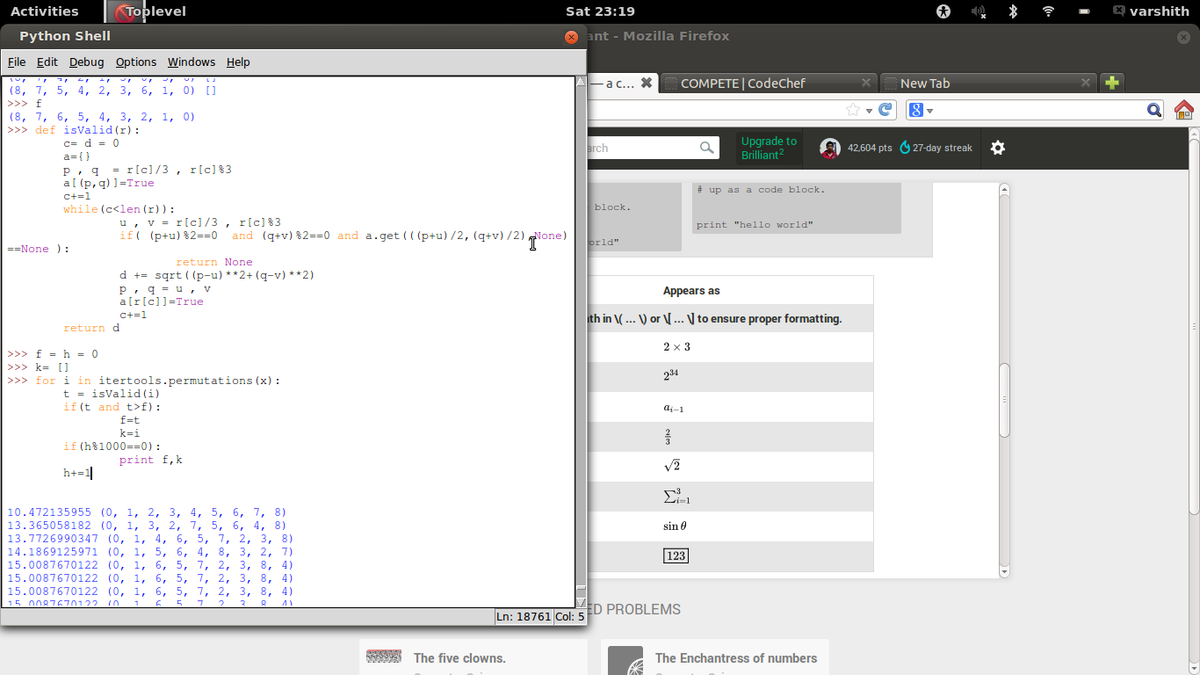
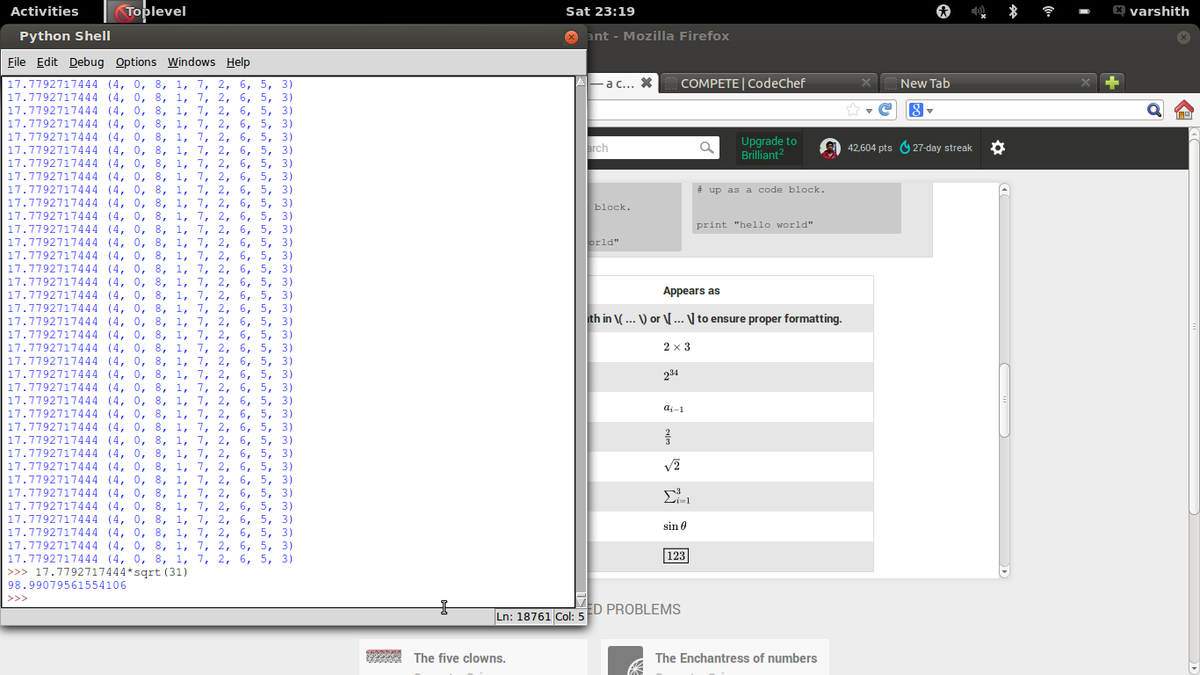
Here is a solution in python 3.4:

from math import sqrt
from itertools import permutations
from fractions import gcd

def distance(n, m, k):
    return sqrt(((n%k) - (m%k))**2 + ((n//k) - (m//k))**2)

def pathdistance(p, k):
    return sum([distance(p[i], p[i+1], k) for i in range(len(p) - 1)])

def between(n, m, k):
    dx = (n%k) - (m%k)
    dy = (n//k) - (m//k)
    dh = gcd(dx, dy)
    dx = dx//dh
    dy = dy//dh
    return [ (n%k)+ i*dx + k*((n//k) + i*dy) for i in range(1, abs(dh))]

def validpath(p, k):
    for i in range(len(p) - 1):
        for n in between(p[i], p[i+1], k):
            if n not in p[0:i]:
                return False
    return True


def solve(k):
    "I promise I won't look"
    dmax = 0
    for path in permutations(range(k*k)):
        newdist = pathdistance(path, k)
        if dmax < newdist:
            if validpath(path, k):
                dmax = newdist
    return dmax

print(round(solve(3)*sqrt(31)))

Varshith Reddy
Jun 28, 2014

I had problems editing the code. So i will just post the picture. The algorithm is

The answer is

sry for replying here but when posting solution (it was incorrect , so after solving problem in code , it came out to be right, and now i cant post solution ) fit is coded in VB.Net and can be downloaded from :- link to download code :- Drive (zip file , contains exe as well as code) it goes maximum for pattern 4081172653 at 98.9907956153453 u can run the code and test it ( code tests all possible combinations for distance so it may take a while ( but if you stop updating of listbox , it may complete bit faster , i have tried to use as less libraries as i can . Code is free for person use , but if you intend to create a tutorial with my code then please give credits to me.

Ninad Sheth - 6 years, 10 months ago

Laurent Shorts
Apr 25, 2016

Here is a possible maximal pattern:

I promise I won't look

Image Credits - stackoverflow, banadia.de

The answer is 99.

3 solutions

0 pending reports