I see a large house and many pets in your future
Fortune tellers use crystal balls to see the future. A fortune teller has a crystal ball with an index of refraction of 1.5 and diameter of 0.2 m. You sit on one side of the ball and the fortune teller sits on the other. She holds up a small red jewel on her side in the equatorial plane of the ball. Let P be the point on the ball nearest to the jewel. How far away in m from P is the image of the jewel on your side?
Hint: the question mark in the image below is an unknown you'll need to figure out as an intermediate step. However, the requested answer is the distance from P , i.e. ? + 0.2 m.
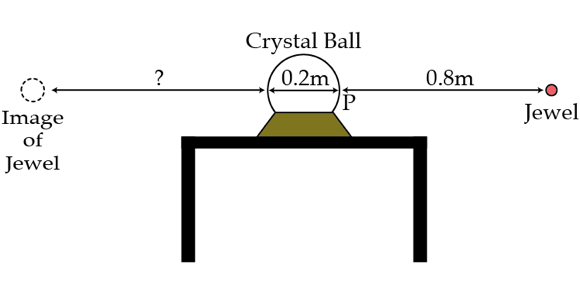
Details and assumptions
- The jewel is at a distance of 0.8 m from P.
The answer is 0.28.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
[Solved using Coordinate Geometry Sign Convention]
Step 1:
Refraction from the first surface:
u = object distance = -0.8 m
v = image distance
n 1 = refractive index of air = 1
n 2 = refractive index of the crystal ball = 1.5
radius(R) = 0.1 m
Using the formula:
v n 2 − u n 1 = R n 2 − n 1
putting the values, we get v = +0.4 m (i.e the image is at a distance of 0.4 m from P on the left hand side)
Step 2:
Refraction from the first surface:
now the image formed from the first surface will act as the object for the second surface.
so, u = +0.2 m (0.4 - diameter of the crystal ball)
v = final image
n = refractive index of air w.r.t crystal ball = 2/3
radius(R) = -0.1 m
Using the formula:
v n − u 1 = R n − 1
putting the values, we get v = +0.08 m (i.e the image is at a distance of 0.08 m from the second spherical surface on the left hand side)
This image is the final image. Distance of the image from P is 0.08 m + 0.2 m = 0.28 m
The focal length of the crystal ball can be calculated from the lensmaker's equation: f 1 = ( n − 1 ) [ R 1 1 − R 2 1 + n R 1 R 2 ( n − 1 ) d ] , where R 1 and R 2 are the radii of curvature of the surfaces of the crystal ball closest to and furthest from the jewel respectively. Plugging in n = 1 . 5 , R 1 = 0 . 1 and R 2 = − 0 . 1 , we obtain f = 0 . 1 5 . Now we apply the formula S 1 1 + S 2 1 = f 1 , where S 1 and S 2 are the respective distances of the jewel and its image from the centre of the crystal ball. Using the values f = 0 . 1 5 and S 1 = 0 . 8 + 0 . 1 = 0 . 9 , we get S 2 = 0 . 1 8 . Since we want the distance of the image from P, we need to add 0 . 1 to our answer to get 0 . 2 8 m.
Consider the sphere as a thick lens, a combination of two spherical refracting surface separated by a distance d=0.2 m. We calculate the focal length
f 1 = ( n − 1 ) ( r 1 1 − r 2 1 + n r 1 r 2 ( n − 1 ) d )
where r 1 and r 2 are the radii of the surfaces.
f 1 = ( 1 . 5 − 1 ) ( − 0 . 1 1 − 0 . 1 1 + 1 . 5 ( − 0 . 1 ) ( 0 . 1 ) ( 1 . 5 − 1 ) 0 . 2 )
f = 0 . 1 5 m
We calculate now the first principal point h 1 , the intersection of the principle plane and the optical axis and the second principal point h 2 , the intersection of the secondary plane and the optical axis. The distances of the object and the image will refer to these points.
h 1 = r 2 n − f ( n − 1 ) d = ( 0 . 1 ) ( 1 . 5 ) − 0 . 1 5 ( 1 . 5 − 1 ) 0 . 2 = − 0 . 1 m
h 2 = r 1 n − f ( n − 1 ) d = ( − 0 . 1 ) ( 1 . 5 ) − 0 . 1 5 ( 1 . 5 − 1 ) 0 . 2 = 0 . 1 m
The points coincide at the center of sphere. Finally we apply
f 1 = s i 1 + s o 1
0 . 1 5 1 = s i 1 + − ( 0 . 8 + 0 . 1 ) 1
s 2 = 0 . 1 8 m
is the image distance from h 2 , the center of the sphere. The distance from P
0 . 1 8 + 0 . 1 = 0 . 2 8 m
The object is placed 0.8 m from the surface of the sphere considering that as the 1st surface we shall calculate as follows The equation for spherical surface is n/V -1/u =( n-1)/R Where n is the refractive index = 1.5 V and u are image and object distance respectively from 1st surface u =- 0.8 (applying sign convention) m R = 0.1 m. , n = 1.5 We get 1.5/V -1/(-0.8)=(1.5-1)/0.1 Solving we get 1.5/V = 3.75 Therefore. V= 1.5/3.75. So V = 0.4 This image acts as a virtual object to the other surface on the opposite side at a distance 0.4 - 0.2 = 0.2 from the second surface. Again using the equation for spherical surface for the second surface we get ( this time the light travels from denser to rarer medium ) So 1/v - 1.5/0.2 = (1-1.5)/-0.1 1/v =12.5 So v = 0.08 this is the distances from second surface Therefore distance from P is 0.28 m
First we use the spherical diopter formula in order to find the distance of the image from the point P caused by the first surface:
1/0.8 + 1.5/x = (1.5 - 1)/0.1 x = 0.4m
So the image caused by the first surface is 0.4m away from this surface on the left, such that the distance of it from the other surface if the sphere is 0.2m, but on the formula we need to change its signal:
-1.5/0.2 + 1/y = (1 - 1.5)/(-0.1)
y = 0.08m
This is the distance of the image from the second surface, so the distance to the point P is given by
z = 0.08m + 0.2m = 0.28m
The thin lens equation states that o 1 + i 1 = f 1
The focal length of a Ball Lens is given by f = 2 ( N − 1 ) R N where R is the radius and N is the refractive index.
Taking the center of ball as the origin, and substituting R = 0 . 1 , N = 1 . 5 : f = 2 ( N − 1 ) R N = 0 . 1 5
Next, we can substitute f and o = 0 . 9 ,into the thin lens equation, to obtain the value i : i = f 1 − o 1 1 = 0 . 1 8
After this, we still have to add 0.1 to the value of o , as the question requested for the distance to the point P, to get o = 0 . 2 8
according to the (z rule) : _____ _____ _____ _______ |__l___|_u1L_| |__a__|_1/a___| |__F1__|___________ -x/u2 |_F2 ___|_____ |_u1L+F2_|1/(u1L+F2)| |(1/a)+F2|__S__|
l=the distance from the surface of the lens to the object
L= l 1
u1=the coefficient of refraction for the medium where the object is located
u2=the coefficient of refraction for the medium between the two lenses
F1=the power of lens1
F2=the power of lens2
x=the distance between the two lenses
a=(1/(u1L+F2))-(x\u2)
S=the distance from the surface of the lens to the image (what we need)
all distances measured from the surface of the lens, so distance in the direction of light is positive and distance in the other direction is negative
F=(u2-u1)* r 1 r=the radius of the lens
then F1=(1.5-1)* 0 . 1 1 = 5 Δ (diopter m 1 )
F2=(1-1.5)* 0 . 1 − 1 = 5 Δ
l=0.8
so we can calculate S at this way
_____ _____ _____ _____ |__1___|__2__| |__5__|_6___| |__F1__|__ -x/u2 |_F2 _|_____ |_3_|__4__| |__7__|__S__|
1 =-0.8 2 =-1.25 3 =3.75 4 =4/15
5 =2/15 6 =15/2 7 =12.5 S =0.08
then the distance we need is 0.2+S=0.28 m
The light rays from the jewel refract twice. Let d = 0 . 1 m be the distance from the jewel to P. The first refraction occurs when the light from the jewel hits the nearest surface of the ball. Let the distance to the virtual image created by this refraction be d ′ . We then have (via usual refraction techniques)
d 1 + d ′ n = R n − 1
where n is the index of refraction and R the radius of the ball. Considering the refraction on the opposite side of the ball we can construct
2 R − d ′ n + x − 2 R 1 = R n − 1
where x is the distance from the image of the jewel to P. We can solve these two equations for x , which yields x = 0 . 2 8 m .
i really liked the title though , sir, i hope u add that (as the fortuneteller) i clr jee by a good rank !! @David Mattingly
solution: Let the symbols used here be defined as follows:
µ 1 → refractive index of rarer medium(air)
µ 2 → refractive index of denser medium(crystal ball)
u → object distance
v → image distance
R → radius of curvature of refracting surface(crystal ball)
The positive and negative sign before u,v and R is for distances measured from the pole of the refracting surface under consideration,along and against the path of light originating from the marble respectively,by convention.
Imagine we cut the crystal ball vertically in the middle,then it will act as a system of two similar half-spherical refracting surfaces.Let us name the right surface as L 1 and the the left surface as L 2 .As given,P is the point on the crystal ball closest to the marble,hence,point P and the marble lie on the principal axis of the refracting surface system.Therefore,P is the pole of L 1 . The formula for refraction through a spherical surface is
v µ 2 − u µ 1 = R µ 2 − µ 1
Applying sign conventions for refraction through L 1 , u=-0.8 m,R=0.1 m, µ 1 = 1 , µ 2 = 1 . 5 . Putting these values in the above equation,we get v=0.4 m.The image formed by L 1 will act as an object for L 2 .Let Q be a point on L 2 diametrically opposite to P.Hence,Q is the pole of L 2 .Distance of image formed by L 1 from Q=0.4 m-0.2 m=0.2 m .Now the refraction will take place from denser to rarer medium,therefore,we have to replace µ 1 by µ 2 and µ 2 by µ 1 in the given refraction formula.Applying sign convention for refraction through L_2, u=0.2 m,R=-0.1 m, µ 1 = 1 , µ 2 = 1 . 5 . Putting these values in the formula,we get v=0.08 m.Thus,the distance of image from P=0.2 m+0.08 m=0.28 m.