A computer science problem by Christian Daang
Maximize z = 2 x 1 − 4 x 2 + 5 x 3 − 6 x 4 given the following conditions: ⎩ ⎪ ⎨ ⎪ ⎧ x 1 + 4 x 2 − 2 x 3 + 8 x 4 ≤ 2 − x 1 + 2 x 2 + 3 x 3 + 4 x 4 ≤ 1 x 1 , x 2 , x 3 , x 4 ≥ 0 .
The answer is 31.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Relevant wiki: Linear Programming
For max z , x 2 and x 4 should be minimum and x 1 and x 3 should be maximum For the Given constraints x 2 = x 4 = 0 The question transforms into a linear optimization problem Now the new conditions are : x 1 − 2 x 3 ≤ 2 3 x 3 − x 1 ≤ 1 x 1 , x 3 ≥ 0 Drawing a graph between x 1 and x 3 will give us a enclosed area One of the corner points of feasible area gives us the max value of z
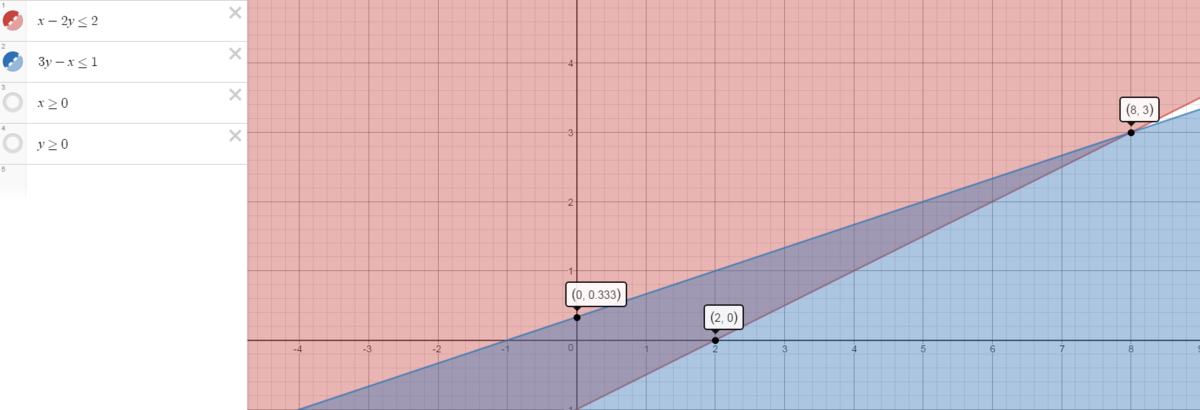
Enclosed area is a quadrilateral with points ( 0 , 0 ) , ( 8 , 3 ) , ( 0 , 3 1 ) , ( 2 , 0 ) Point x 1 = 8 and x 3 = 3 Gives us the Maximum z z = 1 6 + 1 5 = 3 1
I disagree with the first line, or at least it needs to be elaborated further. Why can't we increase x 2 slightly, which results in a greater increase in x 1 , x 3 to make z larger?
Log in to reply
z = 2 x 1 − 4 x 2 + 5 x 3 − 6 x 4 . If we increase x 2 slightly , x 1 also slightly increases but the net increase is negative , because coefficient of x 2 is greater than x 1 . The same applies to x 3 and x 4 . So the best option to maximize z is to put x 2 = x 4 = 0 .
Let A = x 1 + 4 x 2 − 2 x 3 + 8 x 4 ≤ 2 ,
B = − x 1 + 2 x 2 + 3 x 3 + 4 x 4 ≤ 1 .
z = 1 1 A + 9 B − 6 6 x 2 − 1 3 0 x 4 ≤ 2 2 + 9 + 0 + 0 = 3 1 .
Maximised when ( x 1 , x 2 , x 3 , x 4 ) = ( 8 , 0 , 3 , 0 ) .
Standard form of z: − 2 x 1 + 4 x 2 − 5 x 3 + 6 x 4 = 0
Standard form of conditions: { x 1 + 4 x 2 − 2 x 3 + 8 x 4 + x 5 = 2 − x 1 + 2 x 2 + 3 x 3 + 4 x 4 + x 6 = 1
x 1 , x 2 , x 3 , x 4 ≥ 0
x 5 and x 6 are basic variables while the rest x are non-basic variable.
Process involving the 1st table
-5 is the most negative from the coefficients of z.
Negative Ratio is not allowed.
automatic, choose 3, intersection of column x 3 and row x 6 and make it 1 in the 2nd table.
→ x 3 enters the basic variable, x 6 leaves the basic variable.
Make row z, column x 3 and row x 5 , column x 3 zero in the 2nd table.
Process involving the 2nd table
− 3 1 1 is most negative.
5*(row x 3 in the 2nd table) + row z in the 1st table to obtain the results of row z in the 2nd table.
2*(row x 3 in the second table) + row x 5 in the 1st table to obtain the results of row x 5 in the 2nd table.
Negative ratio is not allow, then, automatically, choosing the intersection of row x 5 and column x 1 and make it one in the 3rd table.
→ x 1 enters the basic variable, x 5 leaves the basic variable.
Make row z, column x 1 and row x 3 , column x 1 zero in the 3rd table.
Process involving the 3rd table
11*(row x 5 in the 2nd table) + row z in the 2nd table to obtain the results of row z in the 3rd table.
row x 5 in the 2nd table + row x 3 in the 2nd table to obtain the result of row x 3 in the 3rd table.
→ max x 1 that make z max is 8
→ max x 3 that make z max is 3
→ max z = 3 1 , x 1 = 8 , x 3 = 3 , x 2 = x 4 = 0 .