I Want More Pizza!

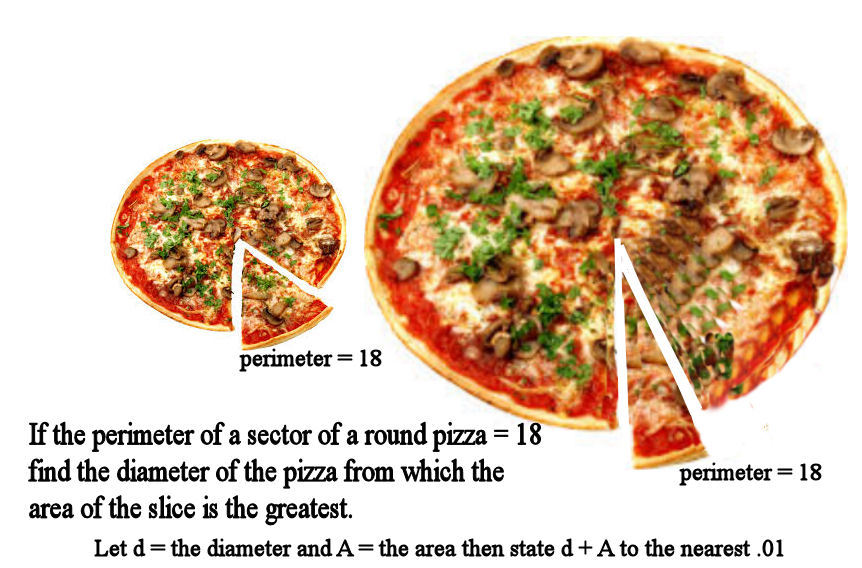
A sector of a circular pizza (area bounded by two radii and an arc) has perimeter 18. What is the maximum area it can have?
Submit your answer as , where denote the diameter and area of the pizza when its area is maximized. Give your answer to 2 decimal places.
The answer is 29.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the angle extended by the sector be θ and the radius of the pizza be r = 2 d . Then, we have:
⇒ A = ( r 1 8 − 2 ) 2 r 2 = 9 r − r 2 ⇒ d r d A = 9 − 2 r
For maximum A : ⇒ d r d A = 0 ⇒ r = 2 9 ⇒ d = 9 ⇒ A = 9 ( 2 9 ) − ( 2 9 ) 2 = 2 8 1 − 4 8 1 = 4 8 1 ⇒ d + A = 9 + 4 8 1 = 9 + 2 0 . 2 5 = 2 9 . 2 5