I want to see more!

First of all, recall the following theorem in this wiki :

There are exactly $\binom{m+n}{n}$ paths from the bottom-left corner to the top-right corner in an $m \times n$ grid.

So, without any restrictions, there are $\binom{3+5}{5}=\binom{3+5}{3}=56$ paths from A to B.

Now, as shown in the diagram to the right, if the path is $A \to A_v \to \cdots \to B_v \to B,$ there is no way for my returning path $B\to A$ not to meet the path $A \to B.$ (You need to convince yourself of this by visualizing the crossing paths in your mind.) So, I need to avoid the path $A_v \to B_v,$ the possible number of which is $\binom{1+5}{1}=6.$

Similarly, if the path is $A \to A_h \to \cdots \to B_h \to B,$ again there is no way for me not to cross the path $A \to B$ on my returning trip. (The subscripts $v$ and $h$ stand for "vertical" and "horizontal", respectively.) So, I need to avoid the path $A_h \to B_h,$ the possible number of which is $\binom{3+3}{3}=20.$

Therefore, our answer is $56-6-20=30.$

However, we can do better by thinking conversely. If I take either the path $A \to A_v \to \cdots \to B_h \to B$ or the path $A \to A_h \to \cdots \to B_v \to B,$ I can always avoid any grid point already visited, on my returning trip.

So, our answer again is $\binom{4+2}{2}+\binom{4+2}{2}=15+15=30.\ _\square$

Either the path from A must go up and be confined to the upper left 2x4 grid then go right to B (thus allowing a return trip along the right-most edge and then along the bottom), or it must go right and be confined to the lower right 2x4 grid, then go up to B (allowing a return trip along the top and then the left-most edge).

So for each case, there are (2+4 choose 4) = (6 choose 4) = 15 paths. Thus there are 15 + 15 = 30 paths in all.

$LaTeX$

There are two cases.

The path is started with the vector (1,0) and ends with the vector (0,1) The path is started with the vector (0,1) and ends with the vector (1,0) If this wasn't the case, you could not get back to A.

There are a total of 8 moves to get to the end for any valid path.

(1,0) _ _ _ _ _ _ (0,1) (0,1) _ _ _ _ _ _ (1,0)

There must be 5 Right movements and 3 Up movements.

For each case, 1 Right movement has already been selected and 1 Up movement has already been selected.

That leaves 4 Right movements and 2 Up movements for each case.

The missing 6 movements for each case comes down to permuting with repetition of 4 Right movements and 2 Up movements.

C(6,4) * C (2,2) for each path

2 * ( C(6,4) * C(2,2) ) = 30

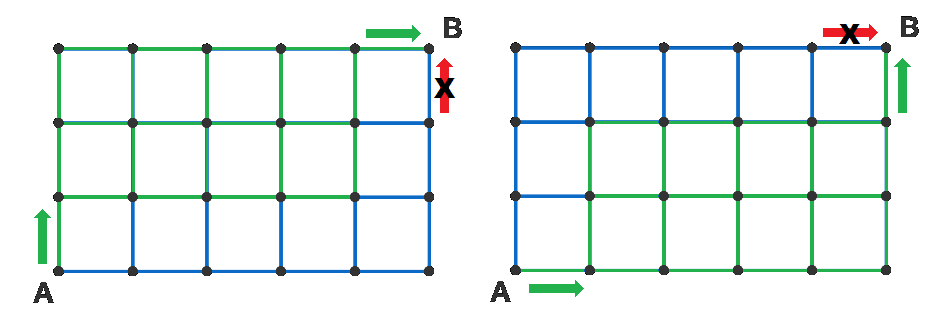
We note that there will be no returnable path if the arrival direction to B is parallel to the starting direction at A . This is because at least the last arrival path to A would have been walked. Returnable paths exist when the starting direction at A is perpendicular to the arrival direction at B .

We also note that the grid of allowable to satisfy the condition is reduce by one column and one row to $4 \times 2$ . And according to Rectangular Grid Walk , the total number of paths is given by $\binom {4+2}2 = 15$ . Since there are two ways to start at A , the total number of such paths possible is $\boxed{30}$ .

We need to leave open one path from A to B open. Such will be going directly left and then up - on the border. That leaves that rectangle because our first move is decided. With the little 2x5 rectangle we have 15 possible paths. The answer is 15x2 because we can revert it.

Consider a particular 2 path from sides of rectangle . As if any another path will be possible then that will also be possible.

Now grid is redused to 2×4 rectangle thus no. Of ways =15 as 2 such paths are possible 2×15=30 such paths fromA--B--A