I was bored, so I started doodling
In the given diagram parabola intersects circle at its vertex point and at one of its roots. The origin is represented by point . If chord is 12 and the equation of parabola can be written as , what is (to the nearest hundredth)?
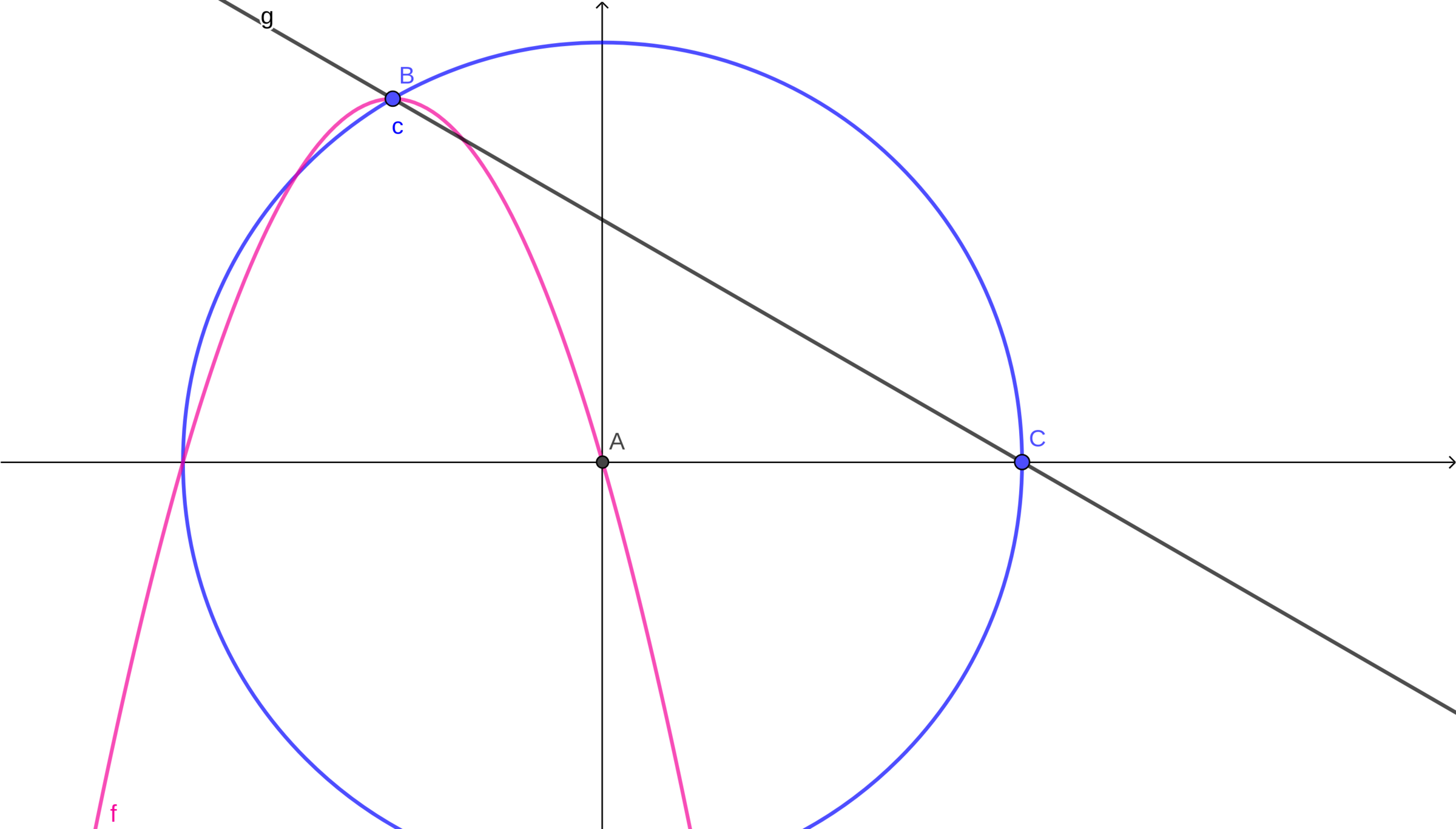
The answer is 3.96.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
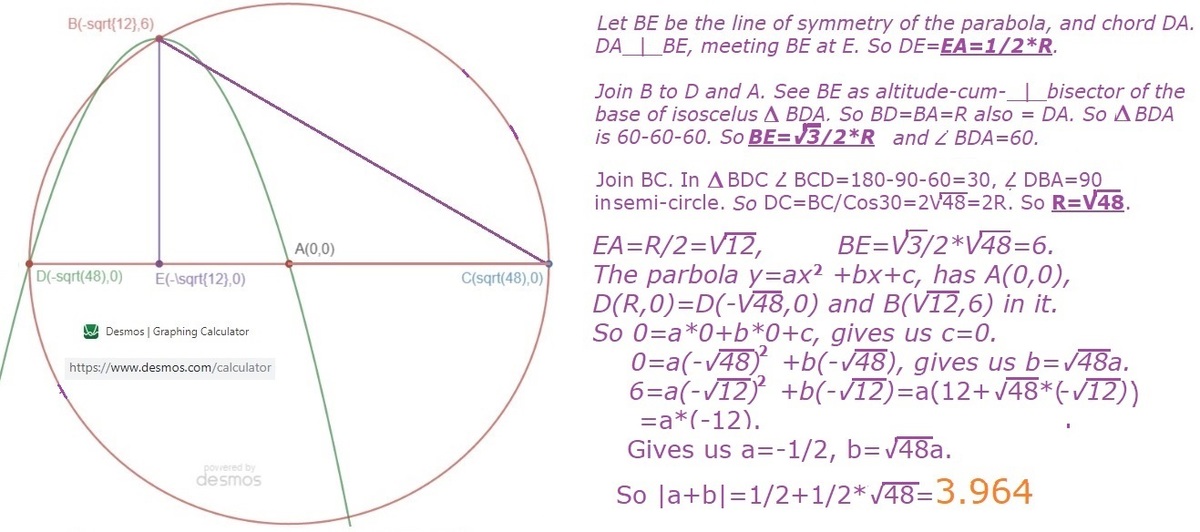
First lets add a few auxiliary lines along with the axis of symmetry.
By creating chord BD and radius AB along with the axis of symmetry, we see that BD ≅ BA, since both are on opposite sides of the axis of symmetry and go from the vertex to one of the parabolas roots. In addition, BA ≅ DA because DA, like BA, is a radius of circle c and all radii are congruent. This also means that BD ≅ DA since both DA and BD are congruent to BA so they must be congruent to each other. From this we can conclude that △ DAB is an equilateral triangle.
Since we know that △ DAB is an equilateral triangle, we know that m ∠ BDA =60. Furthermore, since ∠ DBC is inscribed in a semi-circle it must be 90 degrees. It follows that m ∠ BCD = 30.
Now that we know that m ∠ BCD = 30, we can find the length of BE by doing sin (30)= 1 2 x . By solving for x we find that the length of BE is 6. We can then find BA by doing s i n (60)= x 6 , which in turn gives us the radius of the circle, which is 4 8 .
Now that we have the radius we can get the equation of the parabola. Since the parabola intersects the circle at one of its roots, this means that one of its roots must be 4 8 . Since this intersection occurs in the 2nd quadrant the root is - 4 8 . The other root is at the origin, so we can set up the equation y= a( x 2 + 4 8 x ) . We know we want this parabola to pass through point B (its vertex) so we need to find the coordinates of point B inorder to solve for a. Since the axis of symmetry passes through points B (the vertex) and E (the midpoint of side AD in △ DAB) if we can find the distance from the origin to point E, it's the same as finding the x-coordinate of point B. Since point E is the midpoint of AD in △ DAB, we know that AE must be 2 4 8 . For the x-coordinate of point B the value is - 2 4 8 because the point is in the second quadrant. The y-coordinate is just the length of EB which is 6. Therefore, point B is (- 2 4 8 ,6)
Now that we have point B we can substitute it into our equation and solve for a: y= a( x 2 + 4 8 x )
6 = a( ( − 2 4 8 2 ) + 4 8 ( − 2 4 8 ))
6 = a(12 -24 )
6 = -12a
a = -0.5
Now our equation is y= -0.5( x 2 + 4 8 x ). After distributing we get that b= − 2 4 8 . Finally we can conclude that ∣ a + b ∣ ≈ 3 . 9 6