I wish the Earth wasn't rotating

Classical Mechanics Level 3

If a crate of mass $12kg$ is placed on a weighing machine at a place on earth then calculate the measured weight in SI unit if the rotation of the earth has to be taken into account.

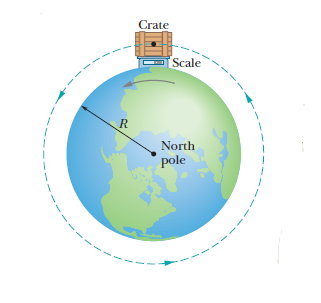
Details and assumption

The acceleration due to gravity $(a_g)=9.806$ $S.I. unit$ .
The angular velocity of the earth $(\omega)=7.292\times10^{-5}$ $S.I. unit$ .
The radius of earth $(r)=6.371\times10^6$ $S.I. unit$ .

If your answer is $x$ , then enter your answer as $x\times10^3$ and round it off to the nearest integer

The answer is 117265.

1 solution

Shreyansh Mukhopadhyay
Jan 29, 2018

In this solution, I have considered the direction towards the outward from the centre of the earth as positive.

The normal force $(F_n)$ on the crate from the scale is directed outward, in the positive direction of r-axis.
The gravitational force, represented with its equivalent $ma_g$ , is directed inward(negative of r-axis). Because it travels in a circle about the center of the earth, as the earth turns the crate has a centripetal acceleration $a_r=\omega^2r$ directed toward the earth's centre(negative of r-axis)

Thus $F_{net,r}=ma_r$

$\Rightarrow F_n-ma_g=m(-\omega^2r)$

$\Rightarrow mg=m(a_g-\omega^2r)$

Putting the values given in question, $mg=117.265N$

So the answer is $\boxed{117265}$

I wish the Earth wasn't rotating

The answer is 117265.

1 solution

0 pending reports