I wish there was a $\displaystyle\sum_{x=0}^{n}$ on the left instead!

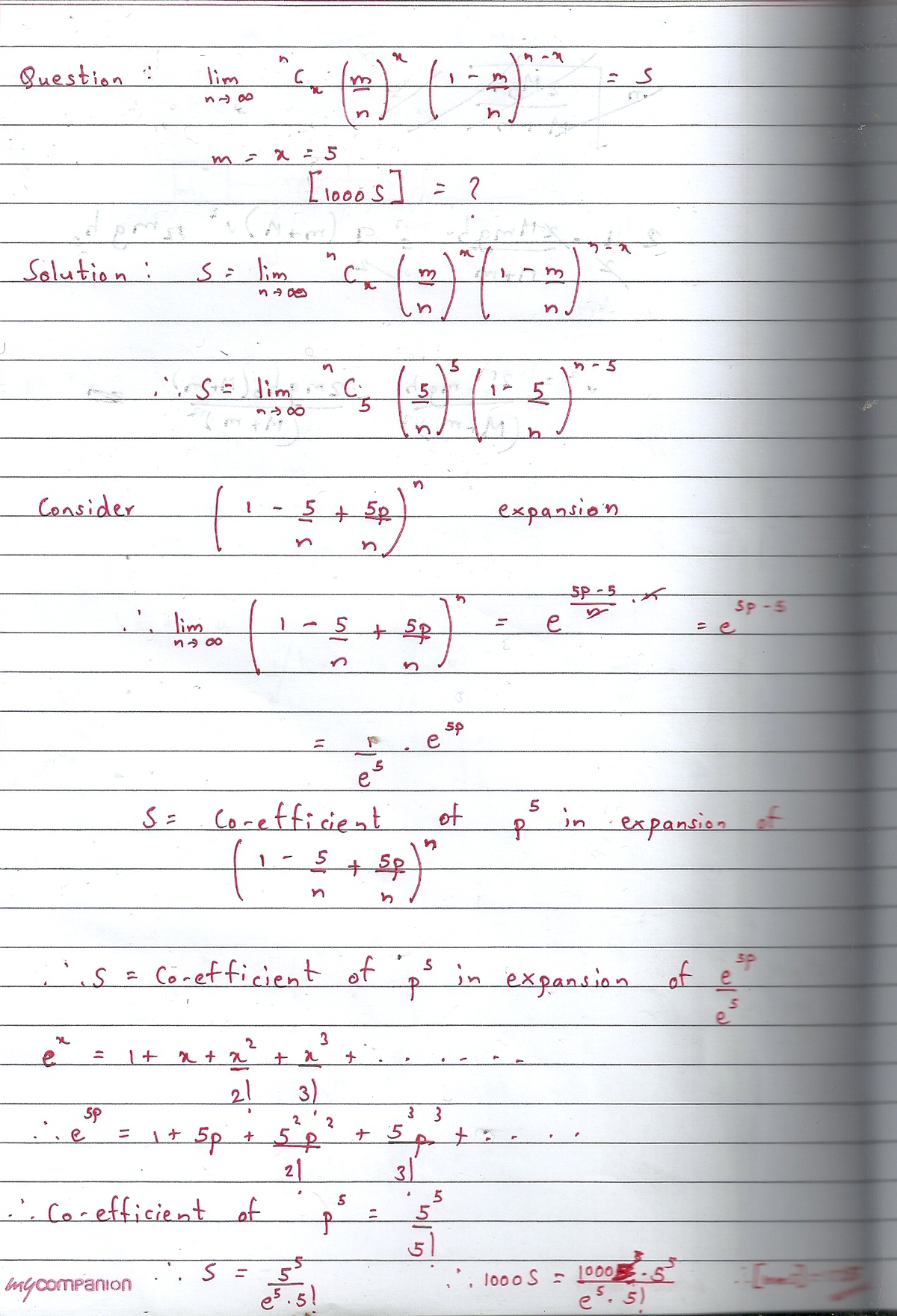
Let's first of all replace $x$ and $m$ with $5$ .

Let's us represent $^{n}C_{5}$ by $C_{5}$ $\lim_{n\to \infty} C_{5}\Bigg( \dfrac{5}{n} \Bigg) ^{5} \Bigg( 1-\dfrac{5}{n} \Bigg) ^{n-5}$ $\lim_{n\to\infty} \dfrac{n(n-1)(n-2)(n-3)(n-4)}{4!} \dfrac{5^{5}}{n^{5}}\dfrac{\Bigg( 1-\dfrac{5}{n} \Bigg)^{n}}{\Bigg( 1-\dfrac{5}{n} \Bigg) ^{5}}$ Distributing the limits over multiplication we get:- $\dfrac{5^{5}}{5!} \lim_{n \to \infty} \dfrac{(n-1)(n-2)(n-3)(n-4)}{n^{4}} \dfrac{\lim_{n\to\infty} \Bigg( 1-\dfrac{5}{n} \Bigg) ^{n}}{\lim_{n \to \infty} \Bigg(1-\dfrac{5}{n} \Bigg) ^{5}}$ Solving Each limit separately we get:- $\boxed{\dfrac{5^{5}}{5!} e^{-5}}$

Use Stirling's approximation. The answer is:

$\boxed{\left(\dfrac{5}{e}\right)^5\cdot \dfrac{1}{120}}$

The result directly follows from Poisson Approximation of Binomial Distribution .