I wonder if you are in a good mod
6 6 6 6 6 6 6
What is the remainder when the above number is divided by 7?
Clarification:
There are a total of seven 6's.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Discussions for this problem are now closed
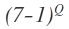where Q is an even integer. On binomial expansion all terms will contain a power of 7 except the last term which will be 1(Because Q is even). Hence remainder must be 1.
6 ≡ ( − 1 ) m o d ( 7 ) ⇒ 6 6 ≡ 1 m o d ( 7 ) ∴ ( 6 6 6 6 6 6 6 ) ≡ 1 m o d ( 7 )
The main reason for the tetration leaving a residue of 1 modulo 7 is not because 6 6 ≡ 1 ( m o d 7 ) . Note that the operation of tetration isn't associative, i.e., in general,
a b c = ( a b ) c
The main fact that I want to express is,
n a = ( a a ) n − 2 a
The reason for the answer is the parity of 6 . Since it is even, any arbitrary exponentiation/tetration of 6 will also be even. And since ( − 1 ) Even value = 1 , we have 6 6 6 6 6 6 6 ≡ 1 ( m o d 6 )
Any power of 6, when "modded" with a base of 7, will equal 1 or 6 depending if the exponent is even or odd. If the exponent is even, the answer is 1 and if the exponent is odd, the answer is 6. Since 6^6^6^6^6^6 (which is the exponent) is even, the answer is 1.
On expanding , we get 6x6x6x6x6......... an even number of times, say n. This can be written as 36x36x36x36x36x36x36........ n/2 number of times. We know that 36=1 (mod 7) Thus the answer is 1
We could directly say that 6 is -1(mod 7) so 6^even number will be (-1)^even number (mod 7) ie 1 (mod 7)
By Euler's Theorem, a y ≡ a y m o d ϕ ( n ) m o d n . Therefore, 6 6 6 6 6 6 6 ≡ 6 ( 6 6 6 6 6 6 m o d 6 ) ≡ 6 0 ≡ 1 ( m o d 7 )
Moderator note:
Although your answer is wrong. You should mention that 6 and 7 are coprime, else your solution is inapplicable.
6 to power any number will give the last digit as 6 therefore when divided by 7 it will give remainder as 1 please correct me if I'm wrong thank you
Moderator note:
This solution has been marked wrong. While it's true to check whether a number is divisible by 2 by checking its last digit, it does not work for any other integers greater than 2 . For example, 3 7 has a last digit 7 but 3 7 is not divisible by 7 .