I wonder what A might be
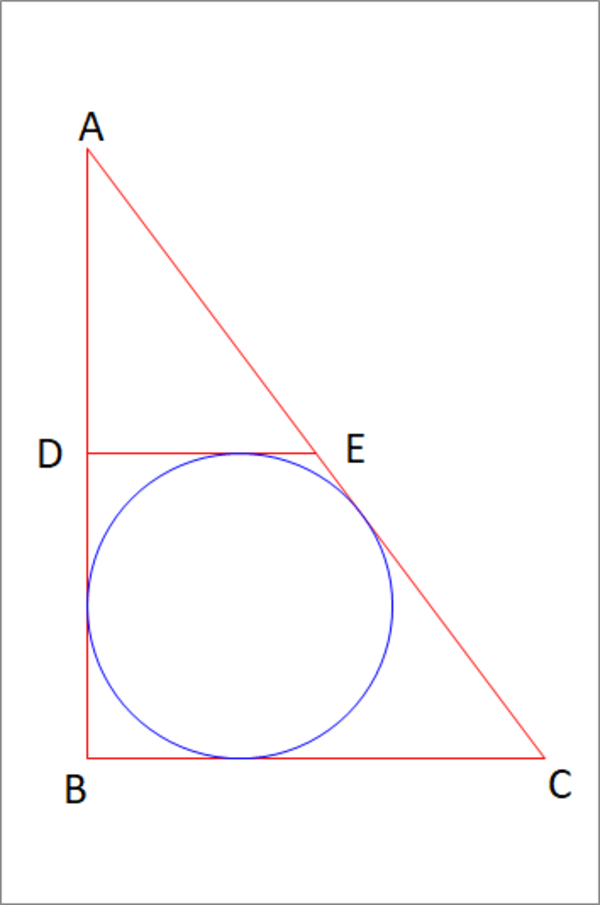
△ A B C is right at B . D E is drawn parallel to B C such that A D = D B . ∠ A is such that we are able to inscribe a circle in trapezoid D B C E that is tangent to all of its four sides. Find tan A
The answer is 0.75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Let A B = 1 and B C = x , so that we are finding tan A = A B B C = x .
Then by the Pythagorean Theorem on △ A B C , A C = x 2 + 1 .
Since A D = D B and A B = 1 , A D = D B = 2 1 , and since the radius of the circle is half the height of trapezoid D B C E , r = 4 1 .
The radius r of the incircle of △ A B C is also r = 2 1 ( x + 1 − x 2 + 1 ) .
Therefore, 2 1 ( x + 1 − x 2 + 1 ) = 4 1 , and this solves to x = 0 . 7 5 .
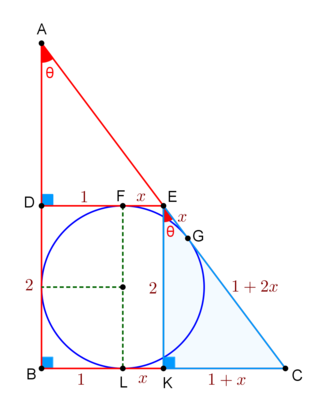 Let the radius of the circle be
r
=
1
and
F
,
G
the contact points of
D
E
and
E
C
with the circle, as seen in the figure. Denote
F
E
by
x
. Then,
D
E
=
1
+
x
,
D
B
=
2
.
Let the radius of the circle be
r
=
1
and
F
,
G
the contact points of
D
E
and
E
C
with the circle, as seen in the figure. Denote
F
E
by
x
. Then,
D
E
=
1
+
x
,
D
B
=
2
.
Since D E ∥ B C and D is the midpoint of A B , it holds that B C = 2 D E = 2 + 2 x .
From E we drop E K ⊥ B C .
Then, E K = D B = 2 , L K = F E = x , B L = D F = 1 and K C = B C − B K = 1 + x .
Furthermore, E G = E F = x (tangent segments) and G C = L C = L K + K C = x + ( 1 + x ) = 1 + 2 x Thus, E C = E G + G C = x + ( 1 + 2 x ) = 1 + 3 x
By Pythagora’s theorem on right △ E K C , E C 2 = E K 2 + K C 2 ⇔ ( 1 + 3 x ) 2 = 2 2 + ( 1 + x ) 2 ⇔ 2 x 2 + x − 1 = 0 ⇔ x > 0 x = 2 1 Consequently, tan A = tan ( ∠ C E K ) = E K K C = 2 1 + 2 1 = 0 . 7 5
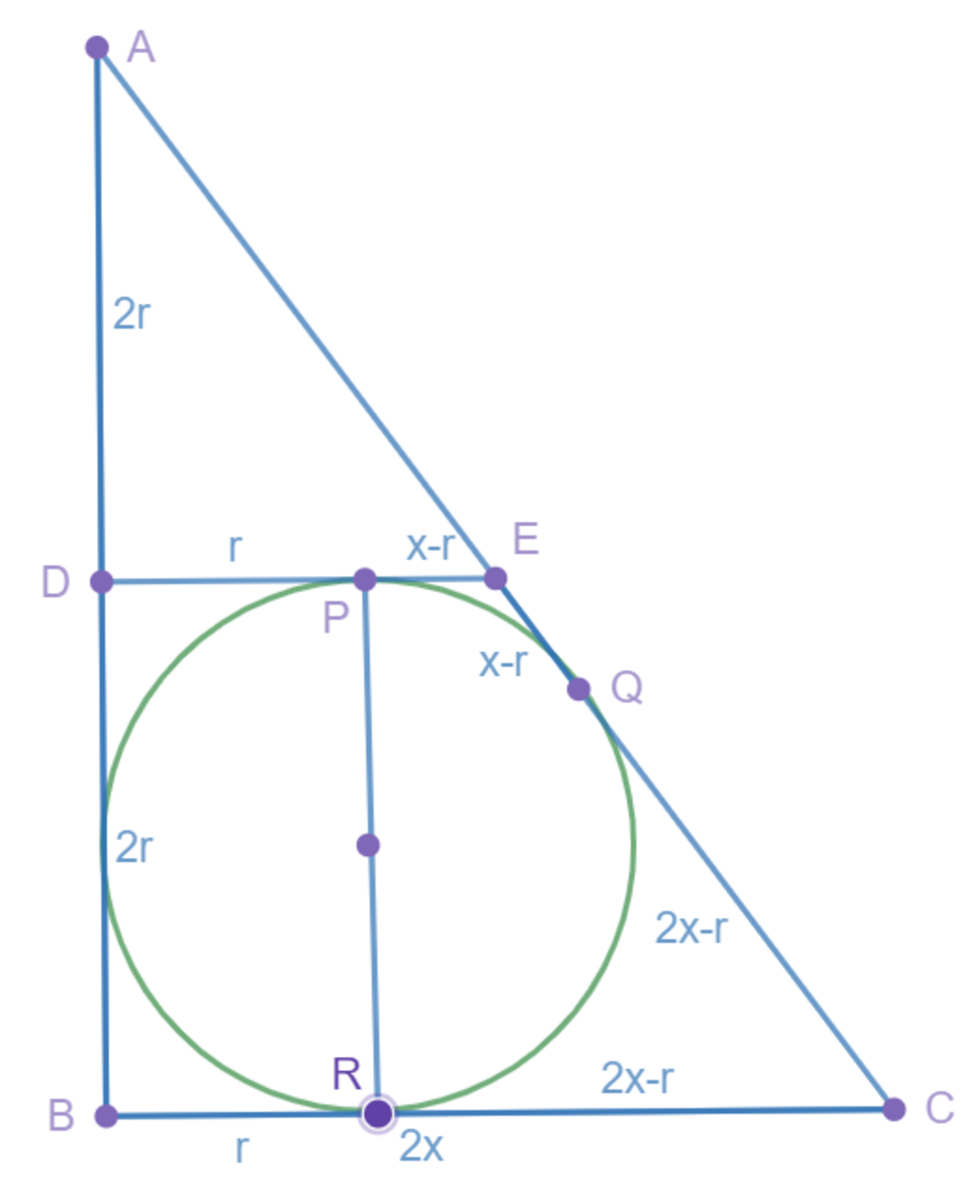
Let the circle's radius be "r", for generality. Let DE = x. Then BC = 2x (midpoint theorem). By inspection, PE = x-r and EQ = PE (equal tangents). Similarly, RC = 2x-r = CQ. Thus EC = EQ + QC = (x-r) + (2x-r) = 3x-2r. By the Pythagorean theorem, AE = ( 2 r ) 2 + x 2 . Since AE = EC, ( 2 r ) 2 + x 2 4 r 2 + x 2 − 8 x 2 + 1 2 x r 2 x − 3 r x = 3 x − 2 r = 9 x 2 − 1 2 x r + 4 r 2 (squaring both sides) = 0 (simplifying) = 0 (dividing by -4x since x = 0 ) = 2 3 r ∴ tan A = A D D E = 2 r 2 3 r = 4 3 = 0 . 7 5
Let A D = D B = 1 . Then D E = tan A , B C = 2 tan A , and the radius of the circle r = 2 1 . We note that
r + cot ( 2 9 0 ∘ − A ) 2 1 + 2 1 cot ( 4 5 ∘ − 2 θ ) 2 1 + 2 1 ⋅ 1 − t 1 + t 2 1 ⋅ 1 − t 2 1 + t t ⟹ tan A = B C = 2 tan A = 1 − t 2 2 ⋅ 2 t = ( 1 + t ) ( 1 − t ) 4 t = 4 t = 3 1 = 1 − t 2 2 t = 2 ( 1 − t ) 1 = 4 3 = 0 . 7 5 Let t = tan 2 A . . . ( 1 ) Note (1): 1 − t 1 = 1 − t 2 4 t