I won't possibly throw like that, would I?
Ball A of mass 1 kg is thrown at an angle of 4 5 ∘ with the horizontal with kinetic energy 5 0 J such that it hits ball B of the same mass placed on the top of a pole. In this collision, half of the kinetic energy of ball A at that instant is transferred to ball B , causing ball B to move in a forward direction. If it is known that the height at which ball B was placed is the maximum height that the initial projectile of ball A would have traveled, then find the distance of the final position of ball B from the foot of the pole.
The figure below would help in understanding the situation:
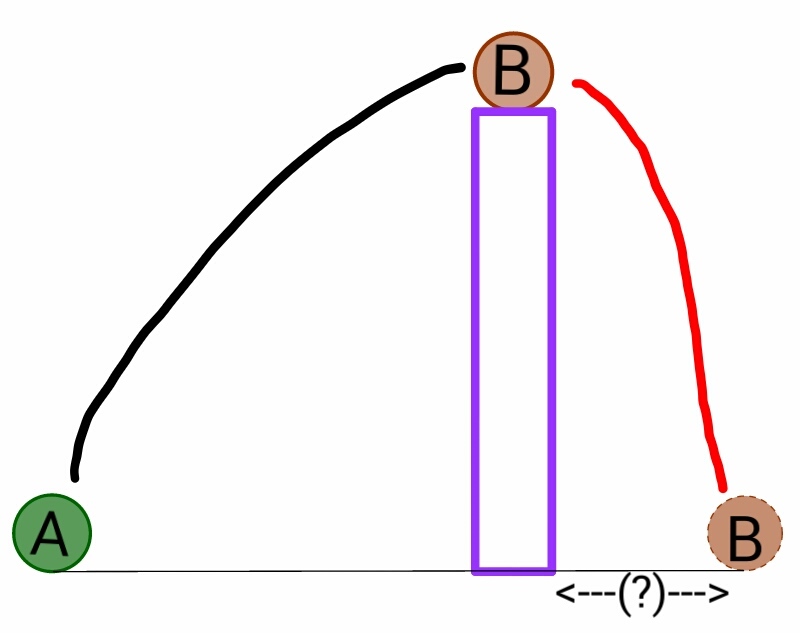
Details and Assumptions:
- Ball B does not rebound after hitting the ground.
- Air friction is negligible.
- Take g = 1 0 m/s 2 as the acceleration due to gravity.
- Give your answer (in m ) to two decimal places.
The answer is 3.54.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
This is a fantastic problem. Simple and yet challenging
I missed the answer, but would like to give my method below.
Since the angle is 45 degrees, Sin45=Cos45, and the Vertical and Horizontal velocities, and so K.E. in these directions will also be equal.
H
o
r
i
z
o
n
t
a
l
d
i
r
e
c
t
i
o
n
h
,
V
e
r
t
i
c
a
l
d
i
r
e
c
t
i
o
n
v
.
B
e
f
o
r
e
c
o
l
l
i
s
i
o
n
K
E
A
h
=
2
1
∗
5
0
=
2
5
J
=
2
1
∗
m
∗
V
A
h
2
=
2
1
∗
V
A
h
2
.
∴
V
A
h
=
5
∗
2
m
/
s
A
l
s
o
t
h
e
h
e
i
g
h
t
h
r
e
a
c
h
e
d
i
s
,
h
=
m
∗
g
K
E
A
h
=
1
0
2
5
=
2
.
5
m
.
K
E
B
h
=
2
1
∗
2
5
=
2
1
∗
m
∗
V
2
=
2
1
∗
,
V
B
2
.
∴
V
B
=
5
m
/
s
.
T
i
m
e
t
t
o
r
e
a
c
h
t
h
e
h
e
i
g
h
t
2
.
5
=
2
1
∗
g
∗
t
2
∴
t
=
2
1
s
.
∴
D
i
s
t
a
n
c
e
B
m
o
v
e
s
=
V
B
∗
t
=
2
5
=
3
.
5
3
5
5
.
Note:- After collision, KE is half, half. Momentum before and after is NOT the same.
I've done exactly the same way. Can this problem be solved in other ways?
Same solution
i don't think it deserved to be at level 3 just a problem of level 1. wasted my time
Log in to reply
Well, it takes so much time to come up with such a problem. Atleast i am contributing. Happy to see it got 8 likes. Well, criticisms are a part of it. :) Talking about the level, it automatically changes with the number of people solving it right, you dont need to worry about it.
Is'nt this question is overated!!
Log in to reply
u should read my comment at that time this was level 3....
kinetic not kibetic but otherwise great solution!
Log in to reply
Hehe thanks for mentioning the spelling mistake :)
Kinetic energy of ball A = 5 0 J .
Now,
K.E. 5 0 v 2 v = 2 1 mv 2 = 2 1 × 1 × v 2 = 1 0 0 = 1 0 m/s
At the maximum point of trajectory, the vertical component of velocity of ball A becomes zero and what remains is the horizontal component of ball A which is given by v cos θ = 1 0 cos 4 5 ° = 2 1 0 .
Kinetic energy at this point = 2 1 mv 2 cos 2 θ = 2 1 × 1 × 2 1 0 0 = 2 5 J
So, kinetic energy obtained by ball B = 2 2 5 . (Ball B obtains half the kinetic energy of ball A).
Again using the formula,
K.E. 2 2 5 v 2 v = 2 1 mv 2 = 2 1 × 1 × v 2 = 2 5 = 5 m/s .
The height of the pole is the maximum height of trajectory of ball A which is given by 2 g v 2 sin 2 θ = 2 × 1 0 1 0 0 × 2 1 = 2 . 5 m
Since ball B is falling from a height, range of its projectile is given by u g 2 h = 5 1 0 2 × 2 . 5 = 5 2 1 = 2 5 ≈ 3 . 5 4 m