Icosagon Coloring
There are exactly 13 different ways to color each side of a regular hexagon either red or blue (where rotations or reflections of the same pattern are not considered a different way):
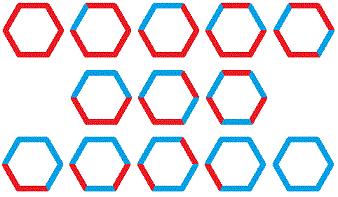
Using the same rules as above, use a computer program to find the number of different ways to color each side of regular 20-gon with just two different colors.
The answer is 27012.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Hi Mark, your explanation is fantastic but it seems very advanced. Can you please explain me in simple terms? This is problem is just fascinating and I am trying since a long time but couldn't get to the solution. Help will be very much appreciated. Thanks a lot in advance.
Log in to reply
I am sorry, but it is not possible to explain this proof unless you have studied some Group Theory, which most people do not do much of until they reach university. If you are interested, you could follow the link to the Brilliant wiki on Burnside's Lemma.
The only low-level proof that I can think of would be to write a suitable computer programme to find all 27012 colourings.
Log in to reply
Sure, that's completely fine Mark. I opened the link but the proof is a bit more complex than I had thought of. I will look into a separate method or learn this later. Thanks for the reply!
Hi @Mahdi Raza , take a look at this link (https://m.youtube.com/watch?v=VOrVMQjQpGg) to get a good grasp of Burnside’s Lemma without any prerequisites ;)
Log in to reply
Thank you for sharing Vedant, very very interesting video. I'll have to watch part 2 and 3. Thanks again!!
You’re welcome!
The following python computer program goes through each possible coloring sequence ( 2 2 0 of them, represented in binary notation) and uses a 2 2 0 boolean item list u to count them. If the sequence's corresponding item in u is false, it hasn't been counted yet, so count it and then make that item in u true and every rotation and reflection item in u true as well.
After running the program, we find that the number of ways to color a regular icosagon with only two colors (where rotations or reflections of the same pattern are not considered a different way) is 2 7 0 1 2 .
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 |
|
hi @David Vreken would you look at my code and tell me why it is so slow
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
|
Log in to reply
I think your code is slower because you are using "id(list(i)) not in l" for each possibility, which is a time-consuming operation. (You may want to try something with boolean values like my program does instead.) Also, if "id(i)" is to be added, you are running the function "id" (unnecessarily) twice.
I also noticed that your program does not eliminate reflected repeats, just rotation repeats. For example, if you make "repeat = 6" in your code to try the given example in the problem, your program comes up with 14 instead of 13, because it incorrectly counts "110100" and "110010" as different possibilities.
This kind of object is known as a bracelet (or free necklace). See
Nice find! The wolfram link references sequence A000029 which gives the answer.
Yes, great connection!!
This is really an Algebra question, since it can be solved by a simple application of Burnside's Lemma : if a finite group G acts on a finite set X , then the number of orbits of this group action is equal to ∣ G ∣ 1 g ∈ G ∑ ∣ F X ( g ) ∣ where F X ( g ) = { x ∈ X : g ⋅ x = x } is the set of elements of X fixed by the group element g .
In this case, let X be the collection of 2 2 0 different 2 -colourings of an icosagon, and let the dihedral group D 4 0 , the full symmetry group of the icosagon, act on X by performing the relevant rotation or reflection to any 2 -colouring. Running through the various elements of D 4 0 :
Thus the total number of orbits is 4 0 1 × 2 2 0 + 8 × 2 + 4 × 2 2 + 4 × 2 4 + 2 × 2 5 + 1 × 2 1 0 + 1 0 × 2 1 0 + 1 0 × 2 1 1 = 2 7 0 1 2
Indeeed, a generalisation of this argument shows us that the number of distinct 2 -colourings of a regular n -gon is 2 n 1 d ∣ n ∑ φ ( d n ) 2 d + 4 3 × 2 2 1 n when n is even, and 2 n 1 d ∣ n ∑ φ ( d n ) 2 d + 2 2 1 ( n − 1 ) when n is odd. The difference between these formulae results from the fact that there is only one type of reflection when n is odd, as opposed to the two types of reflection that occur when n is even.