Icosahedron if rotated
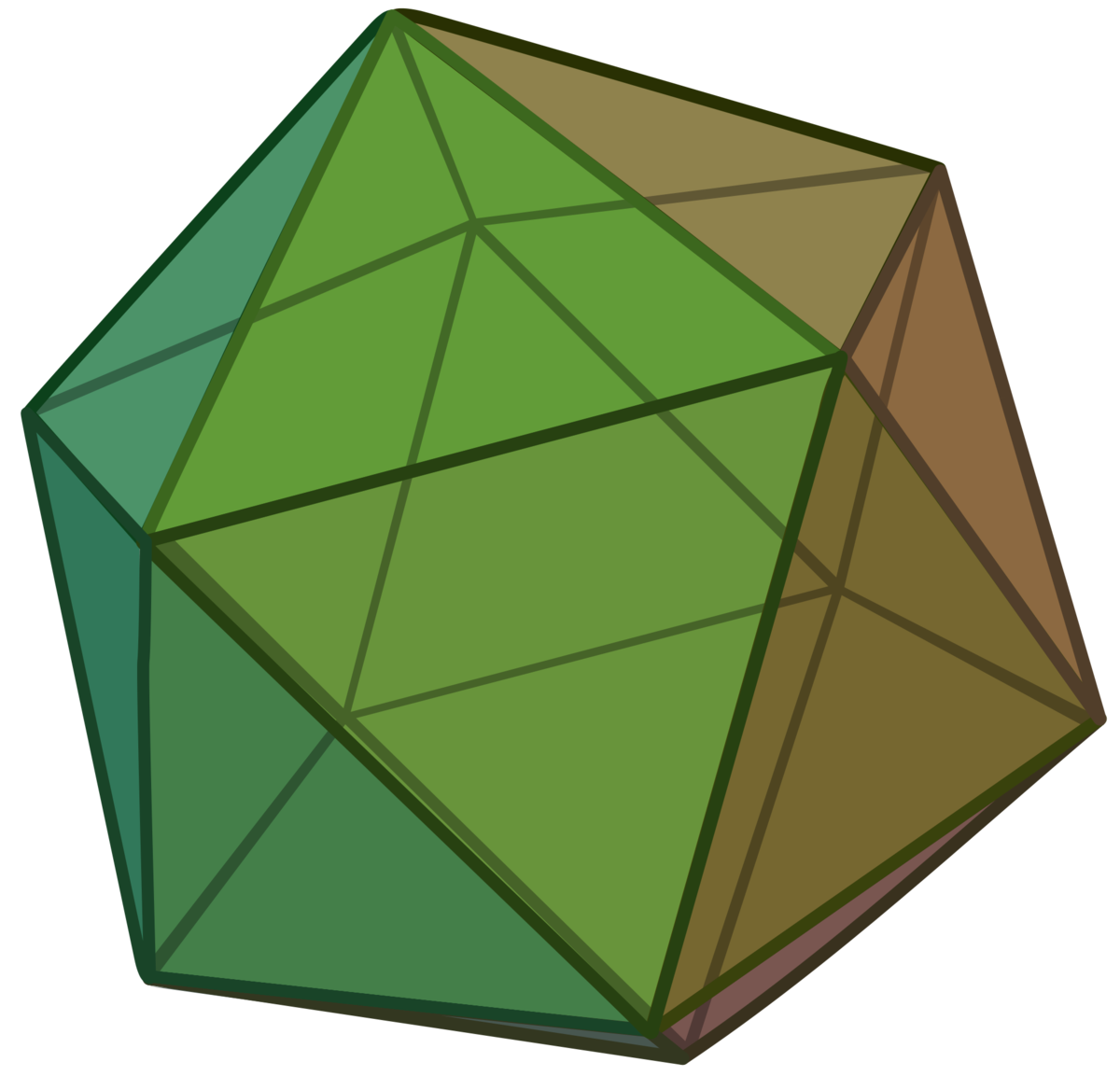
An icosahedron is a regular polyhedron with twenty faces, all of which are equilateral triangles. If an icosahedron is rotated by degrees around an axis that passes through two opposite vertices so that it occupies exactly the same region of space as before, what is the smallest possible positive value of ?
- Submit your answer in degrees.
The answer is 72.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Solution 1 Euler's Formula tells us that V − E + F = 2 , where an icosahedron has V vertices, E edges, and F faces. We're told that F = 2 0 . Each triangle has 3 edges and every edge is common to 2 triangles, so E = 2 2 0 × 3 = 3 0 . Additionally, each triangle has 3 vertices, so if every vertex is common to n triangles, then V = n 2 0 × 3 = n 6 0 . Plugging this into the formula, we have
n 6 0 − 3 0 + 2 0 = 2 ⟹ n 6 0 = 1 2 ⟹ n = 5
Again this shows that the rotation is 5 3 6 0 ∘ = 7 2 ∘ .
Solution 2
Because this polyhedron is regular, all vertices must look the same. Let’s consider just one vertex. Each triangle has a vertex angle of 6 0 ∘ , so we must have fewer than 6 triangles; if we had 6 , there would be 3 6 0 ∘ at each vertex and you wouldn’t be able to fold the polyhedron up. It’s easy to see that we need at least 3 triangles at each vertex, and this gives a triangular pyramid with only 4 faces. Having 4 triangles meeting at each vertex gives an octahedron with 8 faces. Therefore, an icosahedron has 5 triangles meeting at each vertex, so rotating by 5 3 6 0 ∘ = 7 2 ∘ gives another identical icosahedron.