Identical or not?
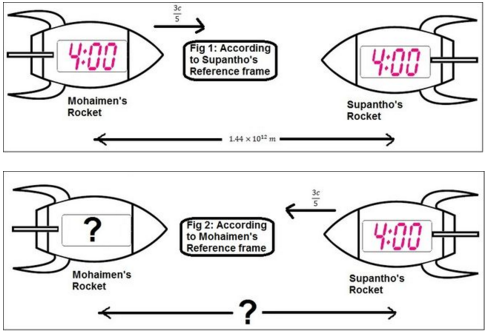 Suppose, Supantho and Mohaimen are moving to each other at a relative velocity of
.
Suppose, Supantho and Mohaimen are moving to each other at a relative velocity of
.
Now, consider the situation in Supantho's reference frame (first figure): The distance between Supantho and Mohaimen is . Both Supantho and Mohaimen's clock show 4:00.
Again, consider the situation according to Mohaimen's reference frame (second figure): Supantho's clock shows 4:00. What will be the distance between them and what does Mohaimen's clock show?
Details and Assumptions
The speed of light is .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's format the problem in a structural way. Look, in this problem, there are 3 events in the spacetime: 1. Supantho in his rocket at 4:00 according to his clock(Fig. 1) 2. Mohaimen in his rocket at 4:00 according to his clock(Fig. 1) 3. Mohaimen in his rocket at time '?' according to his clock(Fig. 2) These 3 events are denoted by P 1 , P 2 , P 3 respectively in fig. 3: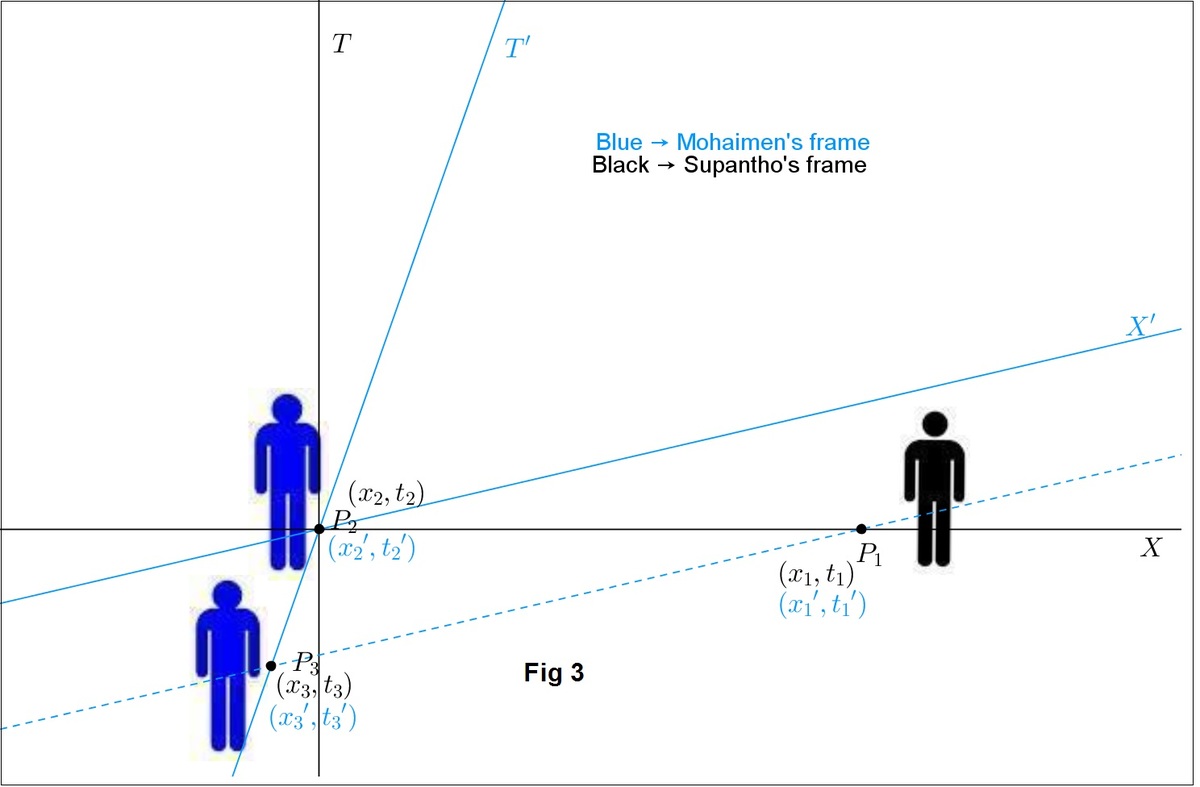 The primed coordinates are of Mohaimen's reference frame, and the unprimed ones of Supantho's (I mean a referance frame which is staionary w.r.t Supantho). I took
P
2
on the origin of both reference frames, so,
x
2
=
x
2
′
=
x
3
′
=
0
t
2
′
=
t
2
=
t
1
=
0
t
3
′
=
t
1
′
x
1
=
1
.
4
4
×
1
0
1
2
m
We have to calculate
x
1
′
&
t
3
′
;
Using Lorentz's transformation,
x
1
′
=
1
−
c
2
v
2
x
1
−
v
t
1
=
1
.
8
×
1
0
1
2
m
t
3
′
=
t
1
′
=
1
−
c
2
v
2
t
1
−
c
2
v
x
1
=
−
3
6
0
0
s
=
−
1
h
r
So the time would be 1 hour less than 4:00, that is 3:00.
The primed coordinates are of Mohaimen's reference frame, and the unprimed ones of Supantho's (I mean a referance frame which is staionary w.r.t Supantho). I took
P
2
on the origin of both reference frames, so,
x
2
=
x
2
′
=
x
3
′
=
0
t
2
′
=
t
2
=
t
1
=
0
t
3
′
=
t
1
′
x
1
=
1
.
4
4
×
1
0
1
2
m
We have to calculate
x
1
′
&
t
3
′
;
Using Lorentz's transformation,
x
1
′
=
1
−
c
2
v
2
x
1
−
v
t
1
=
1
.
8
×
1
0
1
2
m
t
3
′
=
t
1
′
=
1
−
c
2
v
2
t
1
−
c
2
v
x
1
=
−
3
6
0
0
s
=
−
1
h
r
So the time would be 1 hour less than 4:00, that is 3:00.