Identify the Theorem

Geometry Level 1

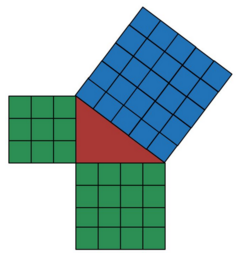
What theorem does this image represent?

Pythagorean Theorem Distance Formula Euler Theorem Einstein Theorem

View wiki
Chung Kevin by Chung Kevin , 45, Australia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

11 solutions

It's the same thing , but worth a mention .

71 Helpful 2 Interesting 0 Brilliant 0 Confused

Moderator note:

Nice GIF, do you have other GIFs that demonstrate Pythagoras Theorem nicely?

This is a GIF by the brilliant team .The GIFs we get when we start a streak .

A Former Brilliant Member - 6 years ago

Very cute & intelligent explanation.. If possible create such explanations for other theorems as well 👍

Rajendra Lekhwar - 5 years, 11 months ago

Also Known as Boudhayana's Sulba Sutra.

Ananya Aaniya - 5 years, 10 months ago

In response to the Challenge Master :

Nope , but I'll try searching for one on Google ;)

A Former Brilliant Member - 6 years ago

Hey Azhaghu its a Cool Gif! ;)

mark chernioglo - 5 years, 10 months ago

ok,, Really Brilliant!1

Parameswaran PG - 5 years, 10 months ago

not only verify the area it also obey the volume

Hariharca Harihar - 6 years ago

Log in to reply

I heard it's a Da Vinci creation , so no doubt it's awesome!

A Former Brilliant Member - 6 years ago
Lee Isaac
Jun 1, 2015

The formula to the Pythagorean Theorem, is that a 2 + b 2 = c 2 a^2+b^2=c^2 , where a, b and c are side lengths of a right angle triangle. Substituting 3, 4 and 5 for a, b and c: 3 2 + 4 2 = 5 2 3^{2}+4^{2}=5^{2}

This formula is used to find the third (unknown) length of a right-angled triangle, when you already know two of the side lengths.

3 Helpful 0 Interesting 0 Brilliant 0 Confused

You should mention that c c is the hypotenuse, because otherwise your solution can be interpreted as saying that c c can be any one of the side lengths, which is not true.

The main idea is that a 2 , b 2 , c 2 a^2,b^2,c^2 represent the area of the squares with side length a , b , c a,b,c respectively and if we measure, we can see that the sum of the areas of the squares made along the non-hypotenuse sides is equal to the area of the square made along the hypotenuse in the diagram.

Prasun Biswas - 6 years ago

Log in to reply

Yes . And could also be mentioned that it is a particular case of general formula that refers to sides and angles. But i don't remember it by heart. Probably somethig about a sen of angle C wich would be 1 or 0

Bruno Pedra - 6 years ago
Steve Varga
Aug 1, 2015

I once dated, Pythagoras' great great great great great great granddaughter... It's all she talked about.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

@Steve Varga for real?

Abdur Rehman Zahid - 5 years, 4 months ago
Ellie-Anne Watts
Dec 11, 2015

At my school we get taught that it is Pythagoras's theorem

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Ananya Aaniya
Aug 1, 2015

The picture is Originally from Boudhayana's Sulba Sutra.. many years prior to Pythagorus.. Please mention the name along with Pythagorus...

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Tanishka Koyande
Jul 16, 2015

Pythagoras theorem shows the squares of the sides

And the cubes given in the figure are perfect squares of 3 , 4 and 5 which is a Pythagorean triplet !

N yeah the gif proves d rest !!

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Look and see... Easy

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Ayush Kumar
Jun 7, 2015

Pythagoras theorem 3^2+4^2=5^2 9+16=25

As number of blocks denote the length of sides

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Josiah Gould
Jun 6, 2015

The distance formula would also work for this because it's just a more generalized form of the Pythagorean theorem. I'm curious if they accepted the distance formula as a correct answer. I went with Pythagorean theorem because it's obvious that's the answer they wanted.

tutorial on the distance formula

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Krishna Garg
Jun 3, 2015

With right angled trianles,This theorem is well known that Square of base + square of height is = sqare of hypotenuse. Thus 3 square + 4 square = 5 square.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Careful with your spelling!

Bonus question : Is Cosine Rule related to Pythagoras Theorem? If yes, which one is the special case of the another? Explain.

Law of cosines is related to pythagorean theorem. Pythagorean theorem is a special case of law of cosines at x = 90, because then anything with cosine in the law of cosines becomes zero (cos 90 = 0)

Hobart Pao - 6 years ago
Luxmi Aggarwal
Jun 2, 2015

As square Of 3 + square of 4= square of 5 This shows pythagorean theorem.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Not quite right. Pythagoras Theorem does not necessarily means that 3 2 + 4 2 = 5 2 3^2 + 4^2 = 5^2 . There are other triplets that all satisfy this criteria: 5 2 + 1 2 2 = 1 3 2 , 7 2 + 2 4 2 = 2 5 2 , 8 2 + 1 5 2 = 1 7 2 5^2 + 12^2 = 13^2, 7^2 + 24^2 = 25^2 , 8^2 + 15^2=17^2 , etc.

Does Pythagoras Theorem only works for right angled triangles?

The Pythagorean theorem works only for right triangles, but not all right triangles are 3-4-5 right triangles. That is to say, the ratios you included would possibly be valid for right triangles with different side lengths.

Also, the theorem only allows you to find the length of the unknown side of a right triangle, but this doesn't necessarily mean that if you have a sum of squares that it must be a right triangle. The theorem is useful if you have the length two of sides and need to calculate the third.

If I remember correctly, in order to calculate the side length of non-right triangles, you need to know the degrees or radians in the opposite angle and the lengths of the other two sides.

Melissa Corbett - 6 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...