Identifying a circle
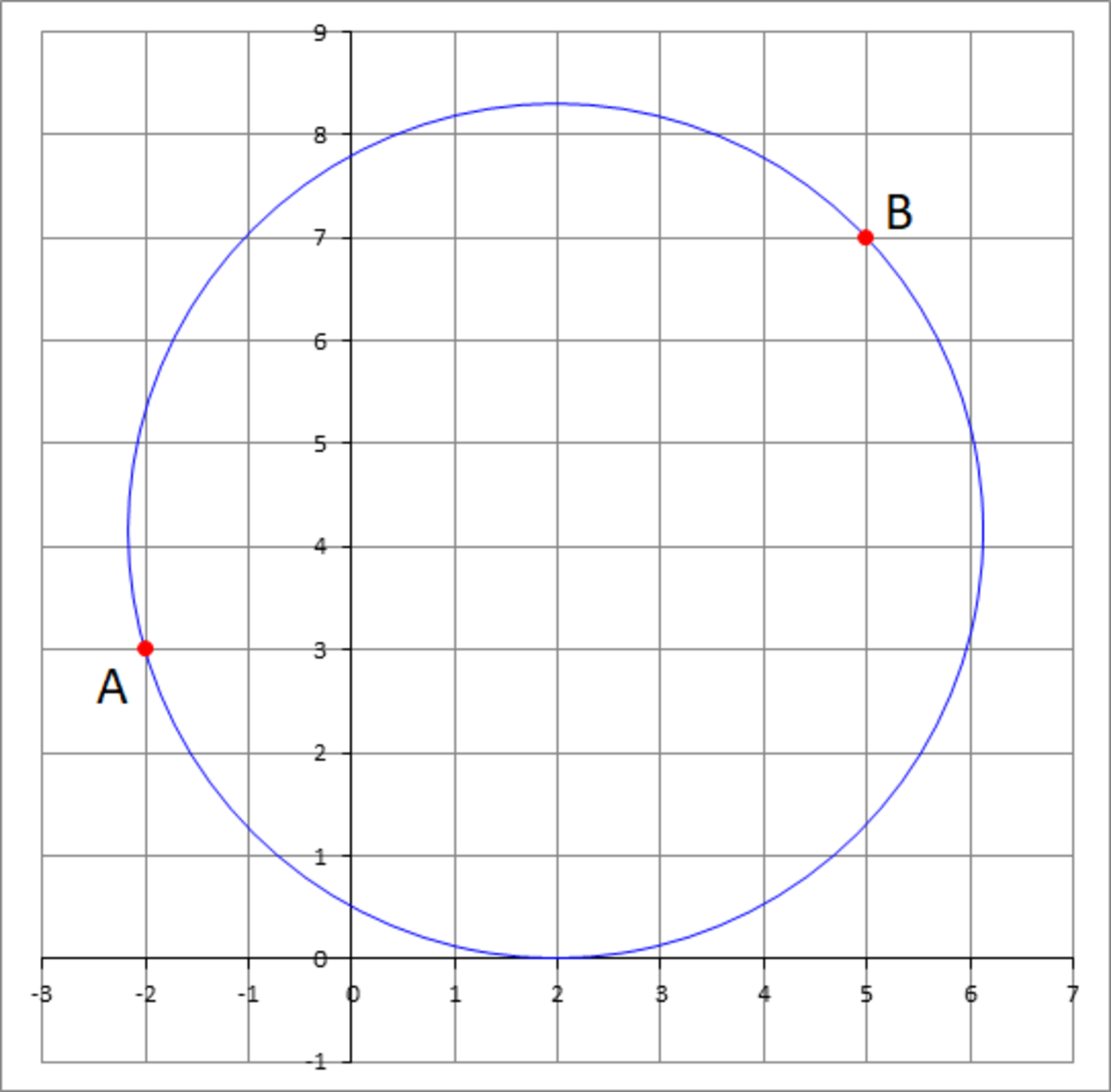
You are given two points: A ( − 2 , 3 ) , B ( 5 , 7 ) , and you are asked to construct the circle that passes through the two points and at the same time be tangent to the x axis. There are two possible circles that satisfy this requirement. Choose the smaller circle and let its radius be R , enter ⌊ 1 0 4 R ⌋ as your answer.
The answer is 41486.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the center of the circle be C ( x , y ) . Since the circle is tangent to the x -axis, its radius is y .
Then by the distance equation, A C 2 = ( x + 2 ) 2 + ( y − 3 ) 2 = y 2 and B C 2 = ( x − 5 ) 2 + ( y − 7 ) 2 = y 2 .
These two equations solve to x = 4 − 2 9 ± 1 3 6 5 and y = 1 6 3 2 5 ∓ 7 1 3 6 5 , the smaller radius being R = y = 1 6 3 2 5 − 7 1 3 6 5 ≈ 4 . 1 4 8 6 7 .
Therefore, ⌊ 1 0 4 R ⌋ = 4 1 4 8 6 .
Let C 1 be the circle in question. We can locate the center C of C 1 as the intersection of two loci:
the perpendicular bisector l of A B , since C is equidistant from A and B and
the parabola C 2 with focus A and directrix the x-axis, since C is equidistant from A and the x-axis.
To find the equation of l , M ( x , y ) ∈ l ⇔ ∣ ∣ A M ∣ ∣ = ∣ ∣ B M ∣ ∣ ⇔ ∣ ∣ A M ∣ ∣ 2 = ∣ ∣ B M ∣ ∣ 2 ⇔ ( x + 2 ) 2 + ( y − 3 ) 2 = ( x − 5 ) 2 + ( y − 7 ) 2 ⇔ 1 4 x + 8 y − 6 1 = 0 ( 1 ) The semi-latus rectum of the parabola is p = d ( A , x ′ x ) = 3 , hence the equation of the parabola is y = 2 p 1 ( x − x A ) 2 + 2 p ⇔ y = 6 1 ( x + 2 ) 2 + 2 3 ( 2 ) Solving the system of ( 1 ) and ( 2 ) we get x = 4 − 2 9 ± 1 3 6 5 , y = 1 6 3 2 5 ∓ 1 3 6 5 The y-coordinate of C corresponds to the radius of the circle as well, thus the smallest circle has radius R = 1 6 3 2 5 − 1 3 6 5 ≈ 4 . 1 4 8 6 7 For the answer, ⌊ 1 0 4 R ⌋ = 4 1 4 8 6 .