Identifying an ellipse
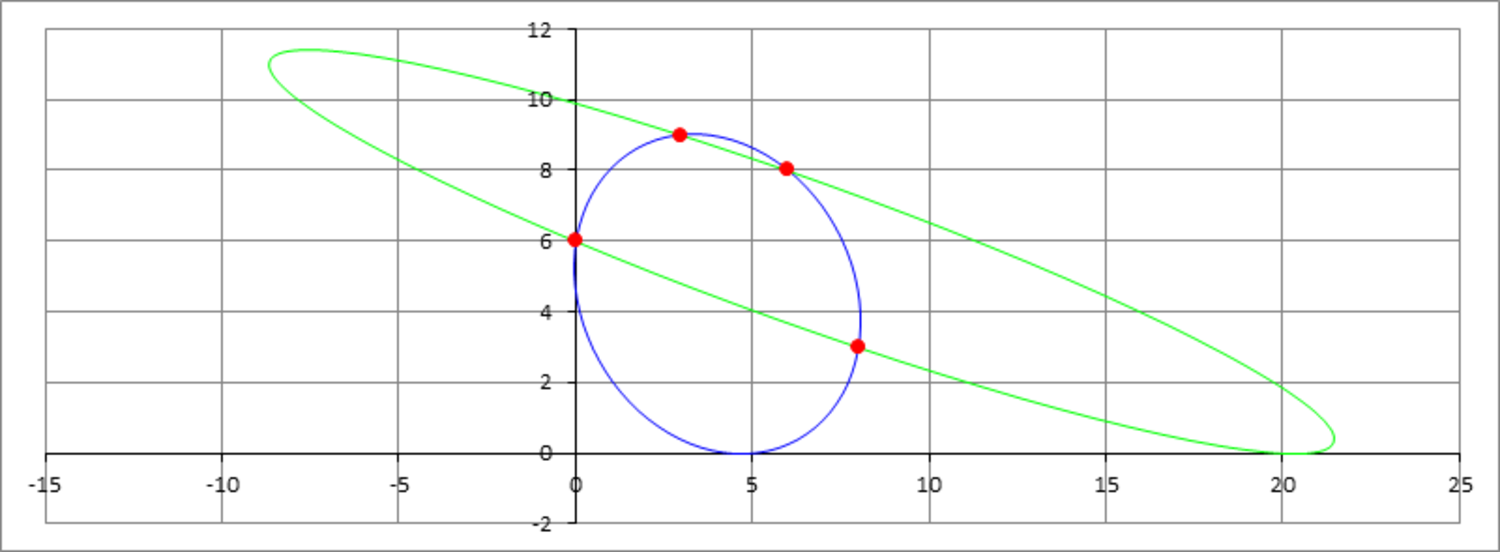
You are given four points: , and you are asked to construct an ellipse that passes through these four points and at the same time be tangent to the -axis. It turns out there are two such ellipses. Find the sum of their areas, and enter as your answer.
The answer is 1586688.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I don't find analytic solution for problem. I use Wolframalpha.
Find ellipse equation in form
a ⋅ x 2 + b ⋅ y 2 + c ⋅ x ⋅ y + d ⋅ x + f ⋅ y = 1
For
y = 0
a ⋅ x 2 + d ⋅ x = 1
D = d 2 + 4 a = 0
a = − 4 d 2
− 4 d 2 ⋅ x 2 + b y 2 + c ⋅ x ⋅ y + d ⋅ x + f ⋅ y = 1
Four equations for points A ( 0 , 6 ) , B ( 3 , 9 ) , C ( 6 , 8 ) , D ( 8 , 3 )
b ⋅ 6 2 + f ⋅ 6 = 1
− 4 d 2 ⋅ 3 2 + b ⋅ 9 2 + c ⋅ 3 ⋅ 9 + d ⋅ 3 + f ⋅ 9 = 1
− 4 d 2 ⋅ 6 2 + b ⋅ 8 2 + c ⋅ 6 ⋅ 8 + d ⋅ 6 + f ⋅ 8 = 1
− 4 d 2 ⋅ 8 2 + b ⋅ 3 2 + c ⋅ 8 ⋅ 3 + d ⋅ 8 + f ⋅ 3 = 1
Solve system
Properties of ellipse 1
Properties of ellipse 2
ellipse1
area enclosed | 102.0215377764767286
ellipse2
area enclosed | 56.64732607727403969317
102.0215377764767286+56.64732607727403969317
Use Wolframalpha
1586688