If one the midpoints ... do I get a parallelogram?

Shown below is a very crudely drawn random-ish quadrilateral, ABCD.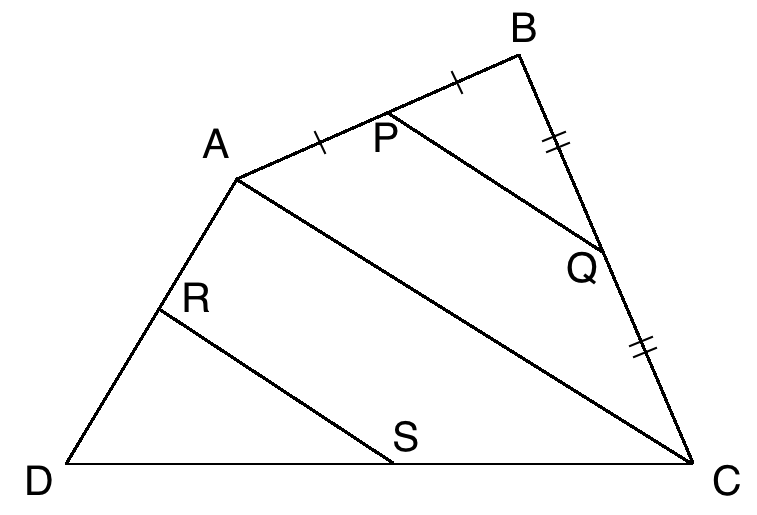 A line has been drawn across the diagonal AC to separate the quadrilateral into two triangles, ABC and ADC, and P, Q, R and S are the midpoints of the sides they are on.

We can see that triangles ABC and PBQ are similar by SAS:

$\angle ABC\,is\,common$

$\frac{AB}{PB}=\frac{CB}{QB}=2$

$∴\triangle ABC \sim \triangle PBQ\,(two\,sides\,in\,the\,same\,ratio\,and\,included\,angle\,equal)$

We can use this to show that the line between the midpoints is parallel to the diagonal:

$∴\angle BPQ=\angle BAC\,(corresponding\,angles\,in\,similar\,triangles\,are\,equal)$

$∴PQ\parallel AC\,(corresponding\,angles\,are\,equal\,on\,parallel\,lines)$

We can then repeat this on the opposite two midpoints with triangle ADC to show that RS is also parallel to this diagonal.

Since both PQ and RS are parallel to AC, PQ is therefore parallel to RS.

We can then repeat this on PR and QS with the other diagonal, BD, to show that PR is parallel to QS

Since each side of the quadrilateral PQSR is parallel to the opposite side, PQSR is a parallelogram, regardless of the shape of ABCD.

The same should apply for concave quadrilaterals, except the two similar triangles would point inwards instead of outwards.

Indeed such a parallelogram is known as (Varignon's parallelogram).