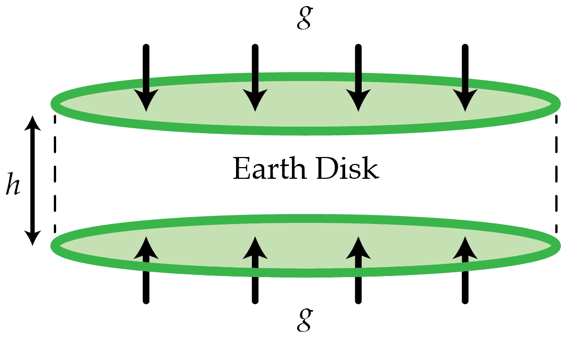
If the Earth were flat...

Using Gauss's law for gravity, $\oint \vec{g} \cdot \mathrm{d}\vec{A}=-4\pi GM_e$ $\rightarrow \boxed{1}$ where $M_e=$ Mass of Earth.

We consider a Gaussian surface of the same dimension of this "earth", thus as $\vec{g}\parallel \mathrm{d}\vec{A}$ , we obtain $g\oint \mathrm{d}A=-4\pi GM_e$ .

Thus $\oint \mathrm{d}A=2\pi R^2$ and $M_e=\pi R^2 h \rho$ .

Substituting these values in $\boxed{1}$ we obtain $h=\dfrac{g}{2 \pi \rho G}$ .

Substituting the given values, we obtain, $h=4251.65$ km $\square$

To start off, Gauss's law for gravity is given by:

$\begin{aligned} \oint \textbf{g} \cdot d\textbf{A} = 4 \pi GM \end{aligned}$

It is given in the problem that the gravitational acceleration is constant: $g = 9.8\space \text{m/s}^2$ It is also clear that the gravitational acceleration vector points in the same direction as the area vector, so the integral evaluates to:

$\oint \textbf{g} \cdot d\textbf{A} = \oint g\space dA = g\oint \space dA = gA = 4 \pi GM$

In this particular problem, $A = 2 \pi R^2$ to account for the areas on both sides, and $M = \rho V = \rho \pi R^2 h$ So we have: $g(2 \pi R^2) = 4\pi G \rho \pi R^2 h$ $h = \frac{g(2 \pi R^2)}{4\pi G \rho \pi R^2} = \frac{2g}{4\pi G\rho}$

Plugging in known values: $h = \frac{2(9.8 \space m/s^2)}{4\pi (6.673\times 10^{-11} m^3 kg^{-1} s^{-2})(5.5\times 10^3 kg/m^3)} = 4.25165 \times 10^6 m = \boxed{4252\space km}$

The acceleration due to gravity near a planet's surface is nothing but its gravitational field intensity near it's surface. Since we know it's value, we will find out a general formula for g at the centre of the top surface and see that it depends on the value of h . From there we will find h.

We see that this thick flat disk of earth, is nothing but similar to a cylinder whose height is h . But we don't know the formula for field strength near a cylindrical mass, but we know that of a disk. So, we will have to consider this cylinder as a series of very thin disks of thickness dy placed on top of another. Each such disk will contribute some field strength at the earth's surface. We will integrate each of these field strengths to get the field strength of the whole disk.

If we take the centre of the top surface of the cylinder as origin 0 and the axis of the cylinder(the vertical line perpendicular to the individual disks) as the y-axis, we can assign the centre of each disk starting from the top a co-ordinate y . Note that y is the distance between a disk's centre and the surface centre where we are to calculate the field strength.

We know that the field strength of a disk of radius a at a pt. at a distance y from it's centre is :

$\frac{2Gdm}{a^2}(\frac{y}{\sqrt{a^2+y^2}})-1$

where dm is the mass of each disk of thickness dh . See that $M=d*pi*(a^2)h$ where d is the given density. Since a is constant, differentiate both sides to get $dm=d*pi*(a^2)dy$

So we get the field strength as: $dg=\frac{2G*pi*d*(dy)}(\frac{y}{\sqrt{a^2+y^2}})-1$

Next step, since y (as well as h ) is very small compared to a as given, $y^{2}$ will be very small compared to $a^{2}$ . So, we can eliminate the y^{2} * in the square root in the denominator. So the expression becomes:

$dg=\frac{2G*pi*d}{a}((y-a)(dy)$

Now, all that is left is to integrate. y will vary from 0 to h. The result will be :

$g=\frac{2G*pi*d}{a}(ah-(\frac{h^2}{2}))$

Since h is very small compared to a , we can eliminate $\frac{h^2}{2}$ because it will be very small, but ah will not be eliminated because a small number times a very large number is still a large number. So:

$g=2G*pi*d*h$ Now, the whole problem reduces to this simple equation. Plug in the values and find h, which will come out in meters. Divide by 1000 to get it in km.

Starting off with the problem is, I think the most confusing part here. You need to a few formulas that denote the Gravitational Field of certain bodies at a particular point.

Such as, The field due to a uniform disk of mass M , of radius R , at a point which is at a distance x from the center of the disk, is \frac{2GM}{R^2} * (\frac{1}{x} - \frac{1}{\sqrt{x^2 + R^2}})

Now, Let us go to a distance x beneath the top surface of the Flat Earth and cut an element of height dx

Hence, this can be considered as a differential disk of mass dm (say) Therefore, The field by this disk at the center of the top surface will be given by replacing M with dm in the above equation.

Now, as we know, dm = \rho * \pi * R^2 * dx

Hence, replacing dm with the given quantity and integrating the field from x running from 0 to h , we get, (E is the gravitational field at the center of the top surface)

E = \int_0^h \frac{2G\rho\pi\R^2}{R^2} x (\frac{1}{x} - \frac{1}{\sqrt{x^2 + R^2}})

Evaluating this integral, we get,

E = 2 G \rho \pi h

Now, its necessary to know that the dimensions of E are that of acceleration and thus, The acceleration at the center of the Flat Earth is equal to E

Hence, equating E with 9.8 m/s^2 we get,

\boxed{h = 4251.65 km}