Real lies where?

Algebra Level 3

Let y = x 2 − 2 x + 4 x 2 + 2 x + 4 \large y = \frac{x^2-2x+4}{x^2+2x+4} where x x can take any real value then y y lies in the interval of:

( 1 3 , 3 ) \left(\frac13,3\right) None of these choices [ − 3 , 1 3 ] \left[-3,\frac13 \right] ( 3 , 3 ) (3,3) [ 1 3 , 3 ] \left[\frac13,3\right]

Ashutosh Kumar by Ashutosh Kumar , 24, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Ashutosh Kumar
Jun 22, 2015

1 Helpful 0 Interesting 0 Brilliant 0 Confused

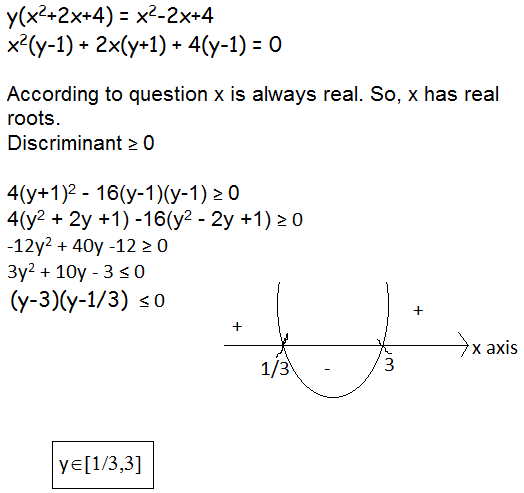
Moderator note:

Simple standard approach.

Bonus question : Evaluate ∏ x = 1 99 x 2 − 2 x + 4 x 2 + 2 x + 4 \displaystyle \prod_{x=1}^{99} \frac{x^2-2x+4}{x^2+2x+4} .

using calculus gives a very nice solution, dy/dx = 0 can be done by quotient rule and since denominator square can never be 0, y = 1 - 4x/x^2+2x+4 => 0 = -4(x^2+2x+4)-(-4x)(2x+2) a quadratic. However, this method gives maxima and minima which are the values of x. so the maximum and minimum value must be checked by putting above obtained values and the 2 extreme values ( both infinites) in above equation. this is much more useful when you have to find values of x for which max or min value occurs or you have a given constraint like x>3.

Bonus: need help, stuck on the way.

Ajinkya Shivashankar - 5 years, 3 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...