Ignorant Grand Piano Movers

Let the weight of the piano be $W$ pounds. If the piano is lifted at either leg $A$ or $C$ , it will tilt slightly and be supported by legs $A,C,D$ alone, essentially be vertical forces of $200,200,W-400$ at $A,C,D$ respectively, while being acted on by a weight $W$ at the centre of mass $G$ . I have made an assumption about the position of $G$ (that it lies "below" $AC$ , so that the piano is not supported at legs $A,B,C$ alone in this case). The assumption is reasonable, given the shape of the piano, and justified by later calculations.

If $G$ has coordinates $(X,Y)$ , taking moments about $D$ gives $\left(\begin{array}{c}60 \\ 0 \\ 0\end{array}\right) \times \left(\begin{array}{c} 0 \\ 0 \\ 200\end{array} \right) + \left(\begin{array}{c}0 \\ 60 \\ 0\end{array}\right) \times \left(\begin{array}{c} 0 \\ 0 \\ 200\end{array} \right) + \left(\begin{array}{c}X \\ Y \\ 0\end{array}\right) \times \left(\begin{array}{c} 0 \\ 0 \\ -W\end{array} \right) \; = \; \mathbf{0}$ and hence $XW = YW = 12000$ .

If the piano is lifted at either leg $B$ or $D$ , it will tilt slightly and (assuming that $G$ lies "to the right" of $BD$ ) be supported by legs $B,C,D$ alone, essentially by vertical forces of $200,W-500,300$ at $B,C,D$ respectively, while being acted on by a weight $W$ at $G$ . Taking moments about $D$ again, $\left(\begin{array}{c}30 \\ 60 \\ 0 \end{array}\right) \times \left(\begin{array}{c} 0 \\ 0 \\ 200\end{array} \right) + \left(\begin{array}{c}60 \\ 0 \\ 0\end{array}\right) \times \left(\begin{array}{c} 0 \\ 0 \\ W- 500\end{array} \right) + \left(\begin{array}{c}X \\ Y \\ 0 \end{array}\right) \times \left(\begin{array}{c} 0 \\ 0 \\ -W\end{array} \right) \; = \; \mathbf{0}$ and hence $XW = 60W - 24000$ and $YW = 12000$ .

Putting these equations together we have $X=Y=20$ and $W = \boxed{600}$ . Since $X=Y=20$ , the centre of mass $G$ is indeed in the region of the piano I have assumed.

I don't know if my solution is correct, but there we go :). I thought that if the piano is lifted a bit, at least one of the other legs will lose the contact to the ground. Since the adjacent sides to the corner where 300 pounds have been measured are equal, two legs will lose contact. Hence the piano will stand on just two legs, which divide the mass among them. Therefore 300 pound is half of the mass and the mass of the piano is $\boxed{600}$ pound.

We can and should assume that the piano is solid, thus as the bottom points of the legs were in a plane (the horizontal plane) originally, they will be in a plane when any leg is lifted to be measured. The diagonal line(s) between the lifted leg and the opposite convex leg(s) (if there were more than 4 legs) dissect the shape spanned by the legs into triangles. The center of gravity is within one of these triangles or within one of the diagonal lines or above one of the legs. Those 3 (or 2 or 1) legs push the ground when a leg is elevated, whose triangle (or diagonal or extreme point) contains the projection of the center of mass to the horizontal plane (because if the center of mass was on the other side of any side of this triangle, the object would rotate). The rest of the legs do not press the ground (either because they do not touch down, or touch but do not weigh).
The sum of the vertical forces to the ground are constant, no matter how the weight of the object is allocated among no matter how many legs. Let a, b, c, d be the original weight forces of the legs (a+b+c+d=W is the weight of the piano, that we seek). We can model the mass of the piano as if it was concentrated into 4 points of the legs. The 4 legs could form a triangle or a concave shape, but our example is simple; the measured leg, the opposite leg and 0 or 1 of the side legs weigh. It is not necessarily the originally heavier side leg that touches the ground, not necessarily the side leg closer to the diagonal between the measured and its opposite leg (and not the side leg closer to the center of mass); but the leg whose product of its original weight and its distance from the diagonal is bigger (if their products are equal that is an equilibrium and none of them weighs the ground: either none of them touches the ground, or any one of them touches the ground without pushing). The original burden of the elevated side leg needs to be allocated among the 3 grounded legs; it should be proven that among only the 2 diagonal legs, and the other side leg does not get anything, no matter what the shape of the triangle is. The original weight of the now elevated leg acts as a counterweight (around the diagonal as axis), decreases the net force of the other side leg, in proportion with the distance of the side legs from the diagonal. This decrease also needs to be allocated among the diagonal legs, but in proportion with the distance of the diagonal legs from the point of the diagonal which is closest to the ground-touching leg.
So let us project the side legs to the diagonal, calculate the ratio of the distances of the diagonal legs from each of these projection points and allocate the burden decrease of the side legs (the elevated side leg lost all its burden, the grounded side leg lost some, because of the counterweight) among the diagonal legs in proportion of the distance ratios. B' := B projected onto the AC diagonal.
D' := D projected onto the AC diagonal.
A' := A projected onto the BD diagonal.
C' := C projected onto the BD diagonal.
B' dissects AC in proportion of 1/4 : 3/4 (just draw a grid of 30' x 30' and see that AB' is half the diagonal of a square of 30' x 30').
D' dissects AC in proportion of 1/2 : 1/2.
A' dissects BD in proportion of 1/5 : 4/5 (ABA', ADA', ABD, DCC' triangles are similar, the ratio of their shorter sides is the same 30:60; AA'=DC'=C'A', BA' is half of them).
C' dissects BD in proportion of 2/5 : 3/5.
When we measure the A leg, its 200 lbs result is a sum of the original a, (B'C/AC=) 3/4 of the totally unburdened b, and (D'C/AC=)1/2 of the push decrease of the D leg (the push decrease of the D leg is (BB'/DD'=) 1/2 of b). a + 3/4 b + 1/2 * 1/2 b = 200
When we measure&lift the A leg, the D leg presses with max(d - 1/2 b; 0); not 300 lbs! You can see this by imagining modifying b until it exactly counterweighs the D leg. Which is bigger: d or 1/2 b: this determines which side leg is elevated.
When we measure&lift the A leg, the C leg presses with c + 1/4 b + 1/2 * 1/2 b, (just as the pendant of calculating the A leg). The constant W remained, b and 1/2 b (that B and D 'lost') were allocated to A and C.

With the same logic when we measure the B leg: b + 4/5 a + 2/5 * 1/2 a = 200 (if A is elevated).
Measuring the C leg: c + 1/4 b + 1/2 * 1/2 b =200, just as when measuring the A leg (a leg exerts the same net force to the ground, no matter if we measure this leg or its opposite leg).
Measuring the D leg: d + 1/5 a + 3/5 * 1/2 a = 300.

Measuring the A or B leg both give a + b =200.
Adding the other two equations: c + d + 1/2 b + 5/10 a = 500 = c + d + 1/2 (a + b); and substituting (a + b) = 200 results 500 = c + d + 100; c + d = 400.
Thus W=a+b+c+d=600 lbs. In reality because of the slight tilting the scale always shows a bit less then the real, so W is slightly more than 600 lbs. Many combinations of a and b; c and d satisfy the measurements and the pair of hypotheses that which side leg is elevated (d>= 1/2 b; a<=2 c).

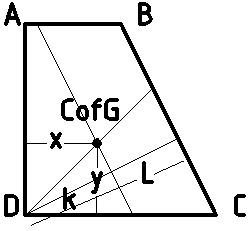
The two measurements at the top edge (A or B) are in fact only one piece of info, since in both cases the piano rests on the scale and the bottom two feet. Reading at A and balancing moments on line CD, with total weight W gives W.y = 200 x 60 (1) Likewise reading at C gives W.x = 200 x 60 (2) Given than x > 0 and y> 0 then Equ 1 / Equ 2 gives x=y which means the CofG lies on a 45° line from D.
Let k be the proportion of the CoG from D to BC. The 45° line intersects intersects line BC at (40,40) from D. So the CoG is at (40k, 40k) from D So W . k . 40 = 200 . 60 (3) Let L be the length of the line from D to BC orthogonal to BC. The weighing at D gives a moment balance about BC (1-k) W L = 300 L (4). Eliminating L and combining (3) & (4) gives. Wk = 300 = (1-k)W (3) By inspection this is k=0.5 (CoG is 20,20 from bottom left corner). And so W = 600

My solution was more geometric. I'm pretty sure my assumptions are in error, but I still got the correct answer:

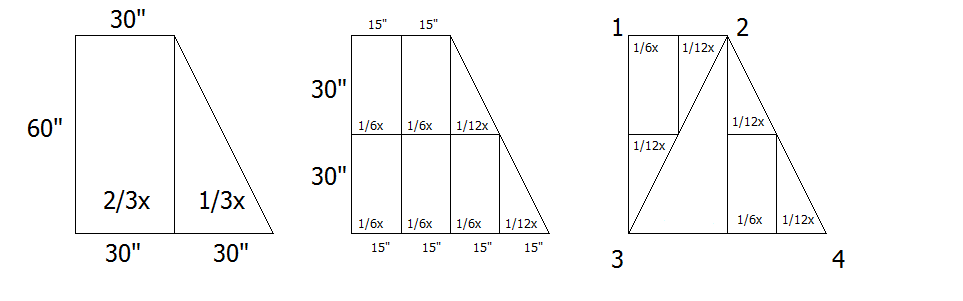
Let x = the total weight of the piano. Assume the weight is evenly distributed.

We can easily divide the shape into 2 areas, showing how the weight is being distributed over the entire piano. If we further divide the shape, we can create triangles of known areas for each leg/corner. I further assumed that legs 1,2, and 3 supported the left rectangle, while leg 4 supported the right triangle. Leg 1 would only support half the weight of the rectangle (1/3 of the total weight) and Leg 4 would support the entire right triangle. From here we could verify that 1/3 total weight was 200, and so the total weight would be 600.

I'm sure this solution doesn't consider 'center of gravity' and my rationale is incorrect, but it's interesting that it still got 600.