IIT-JEE Mains Question
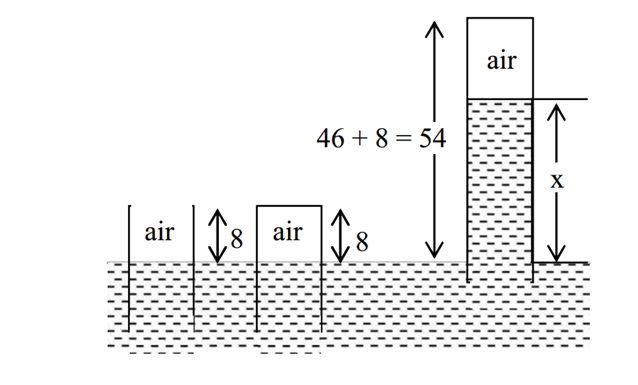 An open glass tube is immersed in mercury in such a way that a length of 8 cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46 cm. What will be the length of the air column above mercury in the tube now?
An open glass tube is immersed in mercury in such a way that a length of 8 cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46 cm. What will be the length of the air column above mercury in the tube now?
(Atmospheric pressure = 76 cm of Hg)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Using Boyle's Law we can find the gas pressure in final condition.
p 1 × V 1 = p 2 × V 2
The volume of the glass tube is equal to A × h
p 1 × A × h 1 = p 2 × A × h 2
p 1 × h 1 = p 2 × h 2
With p 1 is atmospheric pressure, h 1 = 8 c m , and h 2 = 5 4 c m − x
7 6 ( 8 ) = p ( 5 4 − x ) .......... (i)
p + x = 7 6 c m H g ............ (ii)
Substitute p from (ii) to (i), then do some algebra to get
x 1 = 9 2 c m x 2 = 3 8 c m
Since x < 5 4 c m , so x = x 2 = 3 8 c m
The length of air column is 5 4 − x = 1 6 c m