I'll advise you to think twice!
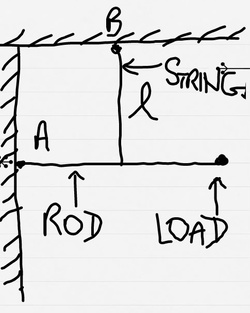A weightless rigid rod with a load at the end is hinged to a point on the wall, so that it can rotation in all directions.
The rod is kept in the horizontal position with the help of an inextensible thread of length , fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure. Determine the period , of the small oscillation of the system.
Let this be given by , where and are coprime positive integers. Find .
Not original.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Let us construct point B', which belongs to the line AB so that point B is the mid point of AB'. It is easily seen that when at rest the load and point B' are on the same vertical line. Besides that the whole line AB' will stay at rest when the rod keeps rotating and during this motion the load will always stay at costant distance 2l from the stationary point B'. Hence one gets SHM of a simple pendulum with the 2l length.