We'll let you guess.
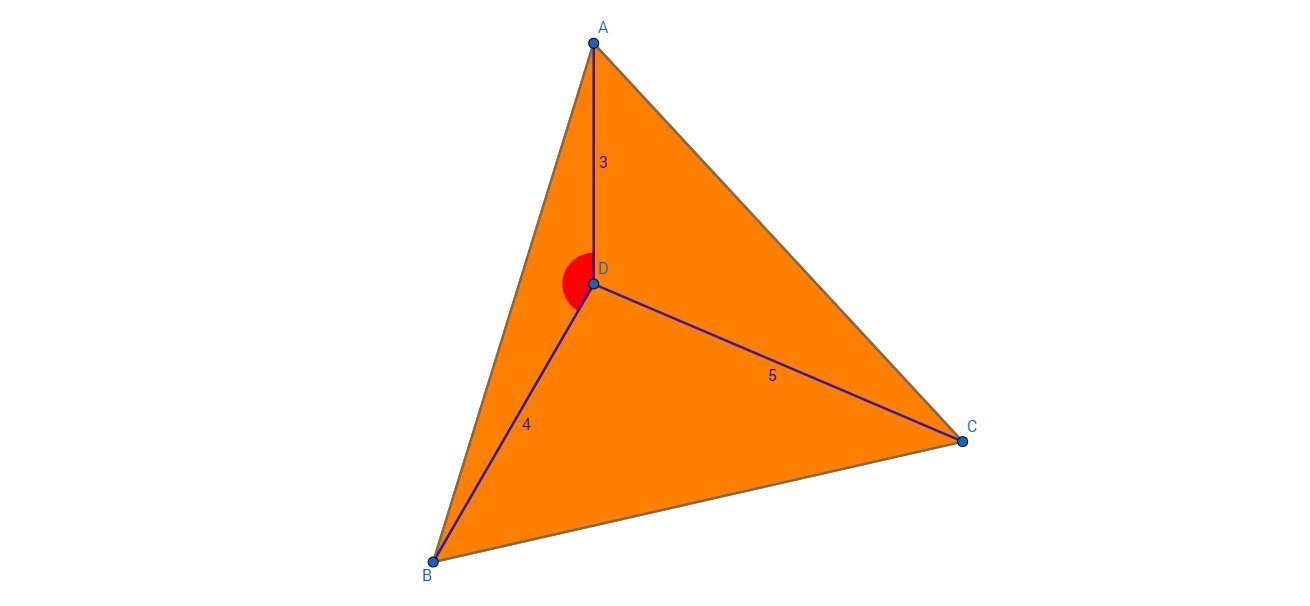 In an equilateral triangle
A
B
C
,
D
is a point such that
D
A
=
3
,
D
B
=
4
, and
D
C
=
5
.
In an equilateral triangle
A
B
C
,
D
is a point such that
D
A
=
3
,
D
B
=
4
, and
D
C
=
5
.
What is the measurement of A D B in degrees?
The answer is 150.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
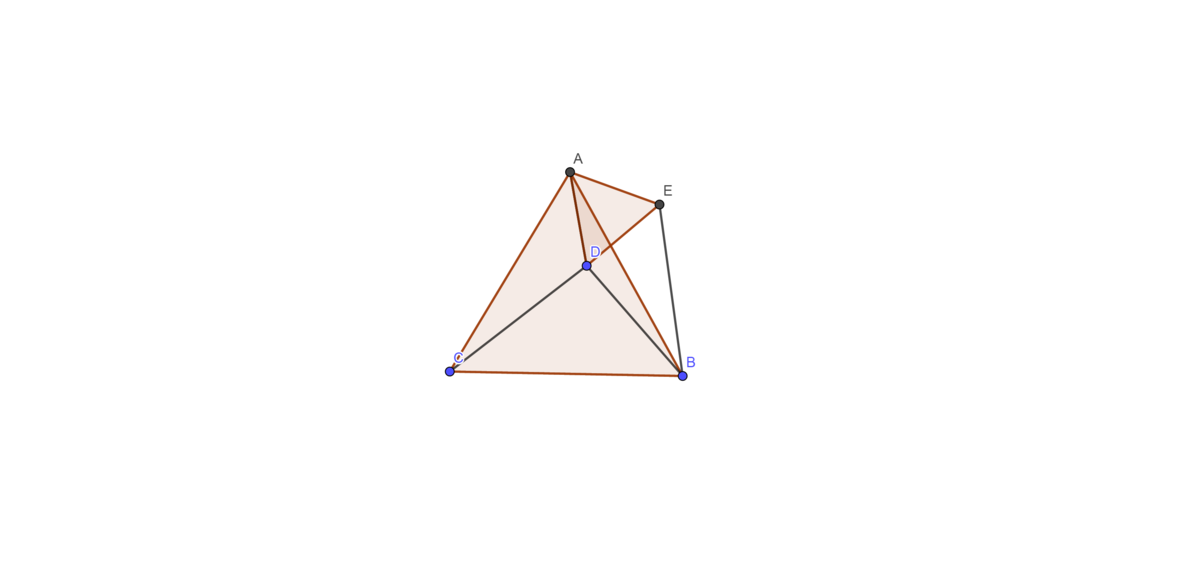
Draw a point E such that ADE is an equilateral triangle (look at the picture). Therefore AE = AD = ED = 3 and E A D = E D A = 60 (degrees).
Since ABC is an equilateral triangle, B A C = 60 (degree) and AC = AB. Therefore, B A D + C A D = B A E + B A D . Hence, C A D = B A E .
Now look at the triangles AEB and ADC. They must be equal to each other because AE=AD; C A D = B A E and AC = AB.
Hence EB=CD=5.
The triangle DEB has DE = 3; DB = 4; EB = 5. According to the Pythagorean theorem, DEB must be a right triangle with E D B = 90 (degrees)
In conclusion, A D B = A D E + E D B = 90 + 60 = 1 5 0 (degrees).
Rotate △ A B C about point A by 60 degrees to form a second triangle, as shown. Then P C = P ′ C ′ = 3 , P B = P ′ C = 5 , and A P = A P ′ = 4 . Because P ′ is the image of point P after being rotated, P A P ′ = 6 0 ∘ . Also notice that A P = A P ′ , so △ A P P ′ must be equilateral. Thus, angle A P P ′ is 6 0 ∘ . Then, because C P = 3 , P P ′ = 4 , and C P ′ = 5 , angle C P P ′ is right. Finally, the angle C P A = C P P ′ + P ′ P A = 9 0 ∘ + 6 0 ∘ = 1 5 0 ∘ .