Illumination

The part of a sphere illuminated by an external light source is a spherical cap (or spherical dome ); there are several formulas for the area of a spherical dome, the one we shall be using is $A=2\pi r^2 (1-\cos\theta)$ , where $\theta$ is the angle between the radius to the top of the cap and a radius to the edge of the cap.

We call the distance from the light source to the centre of the smaller sphere $\alpha$ ; then the distance from the light source to the larger sphere is $18-\alpha$ .

From the diagram above, we see that $\cos\theta_{1} = \dfrac{2}{\alpha}$ and that $\cos\theta_{2} = \dfrac{8}{18-\alpha}$ .

Then, using the formula mentioned above, we have that the combined illuminated area is

$\begin{aligned}A&=2\pi r_{1}^2 \left(1-\cos\theta_{1}\right)+2\pi r_{2}^2 \left(1-\cos\theta_{2}\right)\\ &=8\pi \left(1-\dfrac{2}{\alpha}\right)+128\pi \left(1-\dfrac{8}{18-\alpha}\right)\\ &=8\pi \left[17-\dfrac{2}{\alpha}+\dfrac{128}{\alpha-18} \right]\end{aligned}$

Then setting the derivative equal to zero we get

$\dfrac{dA}{d\alpha}=8\pi \left[\dfrac{2}{\alpha^2}-\dfrac{128}{(\alpha-18)^2}\right]=0$

Dividing by $16\pi$ and simplifying gives us

$\begin{aligned}\dfrac{1}{\alpha^2} &= \dfrac{64}{(\alpha-18)^2}\\ 64\alpha^2 &= (\alpha-18)^2\\ 8\alpha &= \pm(\alpha-18)\\ \alpha &= \dfrac{-18}{7}, 2 \end{aligned}$

Since $\alpha$ must be positive, we discard the first solution. Using $\alpha=2$ , we get

$\begin{aligned}A&=8\pi \left[17-\dfrac{2}{\alpha}+\dfrac{128}{\alpha-18} \right]\\ &=8\pi \left[17-\dfrac{2}{2}-\dfrac{128}{16} \right]\\ &=64\pi\end{aligned}$

Thus the required value of $a \text{ is } \boxed{64}.$

To represent the two spheres, we will consider the equations of two semicircles, one of radius 2 at (0,0) and one of radius 8 at (18,0).

These will have equations $y=\sqrt{4-x^2}$ and $y=\sqrt{64-(x-18)^2}$ respectively.

Now consider 2 x coordinates a and b, each lying within one of the semicircles, and a tangent is drawn from the edge of the circle at x=a or x=b to the x axis: 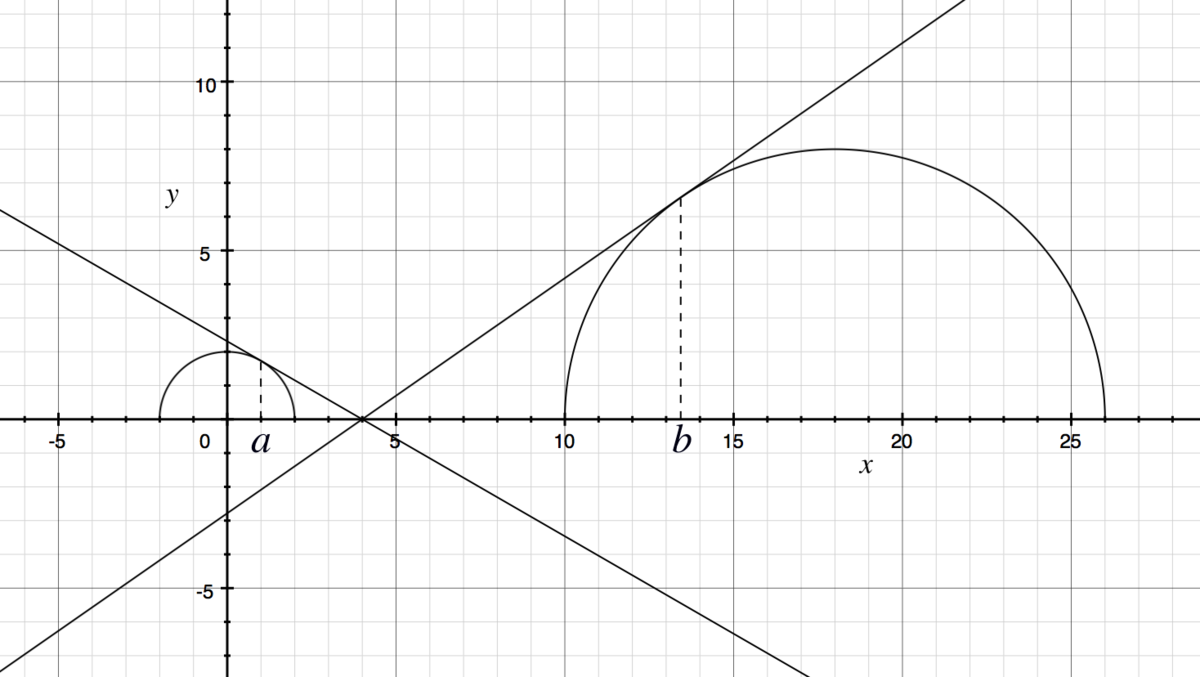We can find the derivative of the equations of the semicircles to get the gradient of this tangent, and subsequently find the equation of the tangents: $\begin{aligned}y&=\sqrt{4-x^2}&y&=\sqrt{64-(x-18)^2}\\ y'&=\frac{-x}{\sqrt{4-x^2}}&y'&=\frac{-(x-18)}{\sqrt{64-(x-18)^2}}\\ y'(a)&=\frac{-a}{\sqrt{4-a^2}}&y'(b)&=\frac{-(b-18)}{\sqrt{64-(b-18)^2}}\end{aligned}$ $\begin{aligned}y-y_1&=m(x-x_1)&y-y_1&=m(x-x_1)\\ y-\sqrt{4-a^2}&=\frac{-a(x-a)}{\sqrt{4-a^2}}&y-\sqrt{64-(b-18)^2}&=\frac{-(b-18)(x-b)}{\sqrt{64-(b-18)^2}}\end{aligned}$ Now in each of these equations of the tangents, we let y=0 to find where they meet the x axis: $\begin{aligned}-\sqrt{4-a^2}&=\frac{-a(x-a)}{\sqrt{4-a^2}}&-\sqrt{64-(b-18)^2}&=\frac{-(b-18)(x-b)}{\sqrt{64-(b-18)^2}}\\ 4-a^2&=a(x-a)&64-(b-18)^2&=(b-18)(x-b)\\ 4-a^2&=ax-a^2&64-b^2+36b-18^2&=bx-18x-b^2+18b\\ ax&=4&18b-bx&=18^2-18x-64\\ a&=\frac{4}{x}&b(18-x)&=18(18-x)-64\\ &&b&=18-\frac{64}{18-x}\end{aligned}$ Now, using these formulas, we can determine the location of a and b for any value on the x axis. To explain fully: we will let x be the position of the light source. The source lights a circular dome on each sphere, but the light only reaches as far as the points whose tangents meet the light source. Since we know where these points are (a and b), we can determine a formula for the total area lit up.

The formula for the area of a dome is $2\pi rh$ where r is the radius of the sphere and h is the height of the dome. The height of the dome on the radius 2 sphere is the distance between a and the edge of the sphere, i.e. $h=2-a$ . The same goes for b, where the edge of the sphere is at 18-8=10: $h=b-10$ . Now we can put all of this into a single formula for the total surface area lit up on both spheres: $\begin{aligned}A&=2\pi(2)(2-a)+2\pi(8)(b-10)\\ &=4\pi\left(2-\frac{4}{x}\right)+2\pi(8)\left(18-\frac{64}{18-x}-10\right)\\ &=8\pi\left(17-\frac{2}{x}-\frac{128}{18-x}\right)\end{aligned}$ Then we simply derive this to find a maximum turning point. $\frac{dA}{dx}=8\pi\left(\frac{2}{x^2}-\frac{128}{(18-x)^2}\right)\\ \text{let }\frac{dA}{dx}=0\\ 8\pi\left(\frac{2}{x^2}-\frac{128}{(18-x)^2}\right)=0\\ (18-x)^2=64x^2\\ 7x^2+4x-36=0\\ \qquad\qquad x=2\qquad(\text{where }x>0)$ Next we would prove that this is a maximum turning point, but this should be elementary for those who know maxima and minima. It's a maximum. It also turns out that this point is actually on the edge of the small sphere, so interestingly we only get the maximum area illuminated if the small sphere is not illuminated at all.

Now we plug this value of x into the formula for the combined area to get the final answer. $\begin{aligned}A&=8\pi\left(17-\frac{2}{2}-\frac{128}{18-2}\right)\\ &=64\pi\end{aligned}$ So the answer is $\boxed{64}$

A light source near a sphere will illuminate a spherical cap , whose surface area is $S = 2\pi rh$ . Below is a diagram of a cross-section of a sphere being illuminated by a light source at $L$ that is $x$ away from the surface of the sphere. Let $r$ be the radius of the sphere, $O$ be the center of the sphere, $C$ be the point of tangency of the sphere, $B$ be the intersection of the $OL$ and the sphere, and $A$ be the perpendicular dropped from $C$ to $OL$ , which makes $AB$ the height $h$ of the cap.

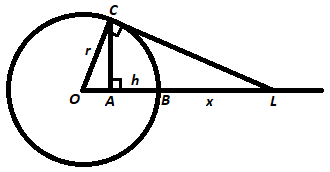
By Pythagorean's Theorem on $\triangle OCL$ we have $CL = \sqrt{OL^2 - OC^2}$ or $CL = \sqrt{(x + r)^2 - r^2}$ or $CL = \sqrt{x(x + 2r)}$ .

$\triangle OCL ~ \triangle LAC$ by angle-angle similarity, so $\frac{AL}{CL} = \frac{CL}{OL}$ , or $\frac{x + h}{\sqrt{x(x + 2r)}} = \frac{\sqrt{x(x + 2r)}}{x + r}$ , which simplifies to $h = \frac{rx}{x + r}$ .

Substituting $h$ into $S = 2\pi rh$ , the surface area of the spherical cap illuminated by the light source is $S = \frac{2\pi r^2x}{x + r}$ .

The total surface area illuminated on both spheres, where the light source is $x$ away from the sphere with radius $r = 2$ , and $y$ away from the sphere with radius $r = 8$ , would then be $T = \frac{2\pi 2^2x}{x + 2} + \frac{2\pi 8^2y}{y + 8}$ .

Since the distance between the surfaces of the two spheres is $18 - 2 - 8 = 8$ , so $x + y = 8$ , or $y = 8 - x$ . Therefore, $T = \frac{8\pi x}{x + 2} + \frac{128\pi (x - 8)}{x - 16}$ .

The function $T$ is always decreasing on the interval $0 \leq x \leq 8$ , so its largest value is at $x = 0$ .

Therefore, the largest surface area illuminated by the light source is $T = \frac{8\pi 0}{0 + 2} + \frac{128\pi (0 - 8)}{0 - 16} = 64\pi$ , which means $a = \boxed{64}$ .