I'm back problem - 3 (Is this just mechanics?)
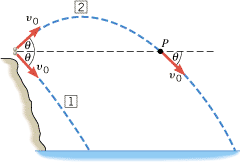 A ball is thrown from the edge of a cliff
high, at an angle of
upward from the horizontal and at a speed of
. Refer to (2) in the figure. Neglecting air friction and other external factors, determine the length
of the path traveled by the ball (depicted in blue dashed lines). Express your answer as
.
A ball is thrown from the edge of a cliff
high, at an angle of
upward from the horizontal and at a speed of
. Refer to (2) in the figure. Neglecting air friction and other external factors, determine the length
of the path traveled by the ball (depicted in blue dashed lines). Express your answer as
.
The answer is 65.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The general equation for a parabolic path is
y = x t a n θ − 2 v 2 c o s 2 θ g x 2
So, we only have to find the horizontal range of the travel, which is given by
x 0 = v c o s θ ⋅ ( g v s i n θ + g 2 v 2 s i n 2 θ + g 1 0 0 )
Then, this will be the upper limit of the length of the travel path, which is given by
A = ∫ 0 x 0 1 + ( y ′ ) 2 d x
where A ≈ 6 5 . 4 9 4 5 , so ⌊ A ⌋ = 6 5