I'm gonna make him an offer he can't resist(ance)
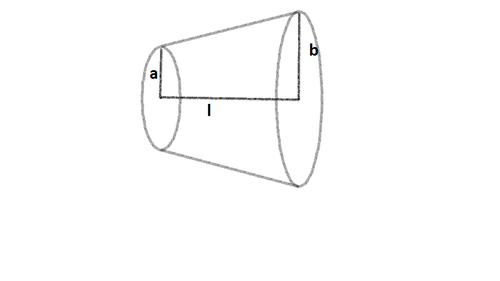 A conductor of length
has a uniform cross section.
A conductor of length
has a uniform cross section.
The radius of cross section varies linearly from to .The resistivity of the material is .
Find the resistance of the conductor across its ends in Ohms .
Details and Assumptions
- = m
- (length of conductor) =10 cm
- =2 cm and =5 cm
The answer is 0.000002.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The resistance of the conductor across its ends is given by: R = ∫ 0 l π r 2 ρ d x
where x is the distance along the axis from the left end and r is the radius of the cross section at x , and r = a + l b − a x = 0 . 0 2 + 0 . 3 x
Therefore,
R = ∫ 0 l π r 2 ρ d x = π ρ ∫ 0 l ( 0 . 0 2 + 0 . 3 x ) 2 d x
= 0 . 3 π ρ [ 0 . 0 2 + 0 . 3 x − 1 ] 0 l = 0 . 3 × 3 . 1 4 1 6 6 . 2 8 × 1 0 − 8 [ 0 . 0 2 1 − 0 . 0 5 1 ]
= 0 . 3 × 3 . 1 4 1 6 6 . 2 8 × 1 0 − 8 × 3 0 = 2 × 1 0 − 6 Ω