I'm not drawing it for you!

Let's calculate the probability of the cycles not intersecting.

By the Pythagorean theorem, the circles won't intersect exactly when the $x$ -values of their centers differ by more than $\sqrt{3}$ .

This is only possible when $A$ is within $2-\sqrt{3}$ from an endpoint of the line segment between $(0,0)$ and $(0,1)$ . Integrating over these values and normalizing by the lengths of the line segments, the probability of the centers not intersecting is

$\displaystyle\frac{1}{2}(\int_0^{2-\sqrt{3}}\frac{2-(x+\sqrt{3})}{2}dx+\int_{\sqrt{3}}^{2}\frac{x-\sqrt{3}}{2}dx)=\frac{1}{2}\int_0^{2-\sqrt{3}}(2-(x+\sqrt{3})dx$

$\displaystyle=\frac{1}{2}\left((2-\sqrt{3})x-\frac{x^2}{2}\bigg|_{0}^{2-\sqrt{3}}\right)=\frac{1}{4}(2-\sqrt{3})^2=\frac{7}{4}-\sqrt{3}$ .

Therefore, $P=1-\left(\frac{7}{4}-\sqrt{3}\right)=\sqrt{3}-\frac{3}{4}$ . We find $10^4P+0.5\approx 9821.01$ , so the answer is $\boxed{9821}$ .

Edit: we could not use calculus by plotting the $x$ -values for $A,B$ and then geometrically finding the area where the circles intersect.

The condition for the two circles to intersect is that the distance between the two centers of the circles should not exceed the sum of the radii of the circles.

So let the center of the first circle be at $(X,0)$ and the center of the second circle be at $(Y,1)$ where $X$ and $Y$ are randomly and uniformly chosen from $[0,2]$ .

Distance between the centers of the circles is :- $\displaystyle \sqrt{(X-Y)^{2} + (1-0)^{2}} = \sqrt{(X-Y)^{2} + 1}$

The sum of the radii of the circles is just $1+1 = 2$ .

Hence the condition of intersection is :-

$\displaystyle \sqrt{(X-Y)^{2} + 1}\leq 2$

Or, $\displaystyle (X-Y)^{2} \leq 3$

So we have the following two dimensional geometrical probability problem in which we have to find $P(\lvert X-Y \rvert \leq \sqrt{3})$ where $X$ and $Y$ are randomly and uniformly chosen from $[0,2]$ .

So solving this graphically we have

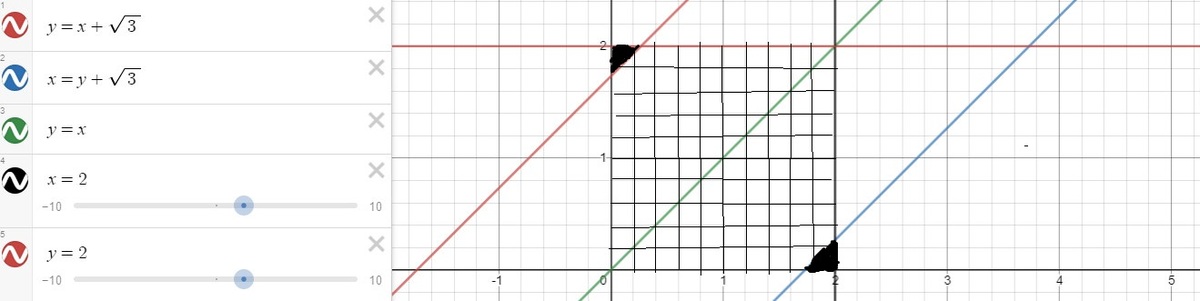
We need the area of the region represented by the grids (I am terrible at drawing) .

So we have the area of each of the small triangles represented by the black shades as :- $\displaystyle \frac{1}{2}(2-\sqrt{3})^{2}$ .

So the area of the grids become :- $\displaystyle 4-(2-\sqrt{3})^{2} =4\sqrt{3} -3$ .

Hence the probability that both the circles intersect is given by the area of the region of grids divided by the total area of the square = $\displaystyle \frac{4\sqrt{3}-3}{4}$