Balancing Act
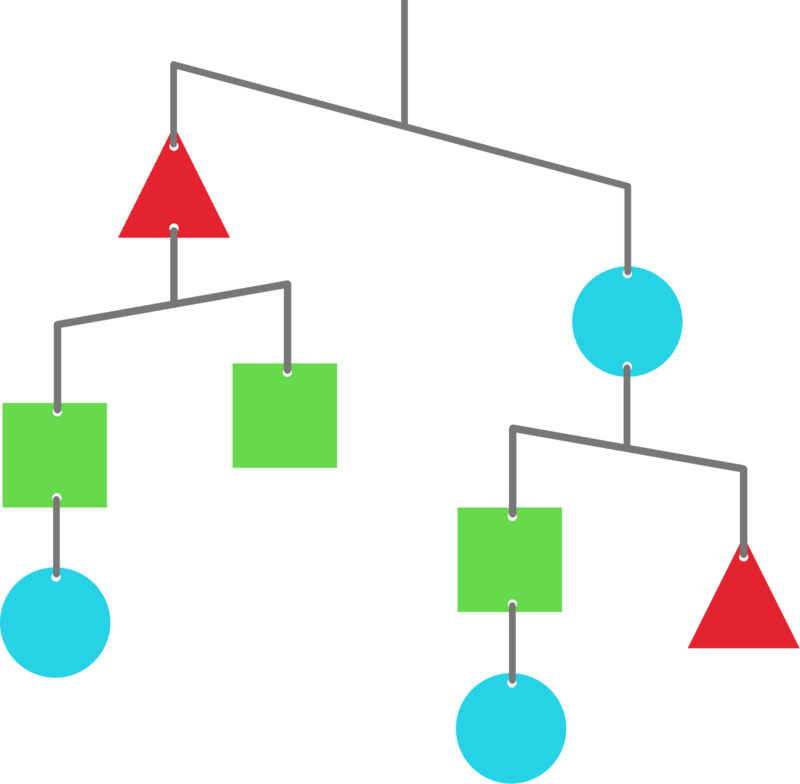The above shows how a mobile will be balanced when left to hang. Assume that the fulcrum is at the center of each rod.
What are the relative weights of these shapes?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
nice answer!!
The bottom left node has rectangle = rectangle + circle. This is only true if circle is weightless.
You really enjoyed these problems. Thanks for writing solutions for them!
Log in to reply
The only issue with this variation of the problem is that there is an unfair imbalance of moments. I.e, the two rods containing rectangle and circle are not perpendicularly equidistant from the highest pivot. But I'm just being picky
amznggg solution ....i really enjoyed this problem
Considering that the fulcrum is where the rod is movable. Don't you think that the weights above would influence the movement of the weights below? How can you be certain which is heavier? What if gravity is pulling it upwards?
Log in to reply
This is an algebraic problem not really a classical mechanics. The balance is used to indicate heavier or lighter only.
Bottom right arms:
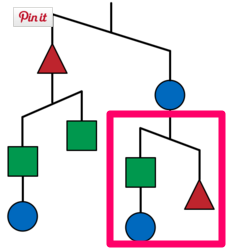
.: Square + Circle <Triangle
Then, it's a process of elimination - like crossing off equivalent things on each side of an equation:
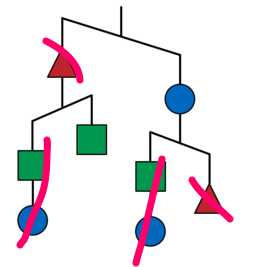
.: Circle > Square
Let me know if my reasoning is sound.
No it is not because you can't cancel objects of two different layers
The root Rod node with right side heavier tells us T r i a n g l e + 2 ∗ S q u a r e + C i r c l e < T r i a n g l e + S q u a r e + 2 ∗ C i r c l e .
Equivalently, C i r c l e > S q u a r e .
Furthermore, we know from the Rod node under the Circle and hanging to the right that S q u a r e + C i r c l e < T r i a n g l e . From this we can infer both that T r i a n g l e > C i r c l e and T r i a n g l e > S q u a r e .
Hence T r i a n g l e > C i r c l e > S q u a r e .
Notice on the lower right branch, the triangle is heavier than the square + circle. If we were to remove a circle, triangle and a rectangle from both side branches, the equilibrium would not change but the remaining circle would be heavier than the remaining rectangle. Therefore, triangle > circle > rectangle.
The right arm > the left arm:
∘ + △ + □ + ∘ > □ + △ + □ + ∘ ⇒ ∘ > □
The bottom of the right arm: △ > □ + ∘
Therefore, △ > ∘ > □