Imbalance Puzzle - Part 3

Algebra Level 1

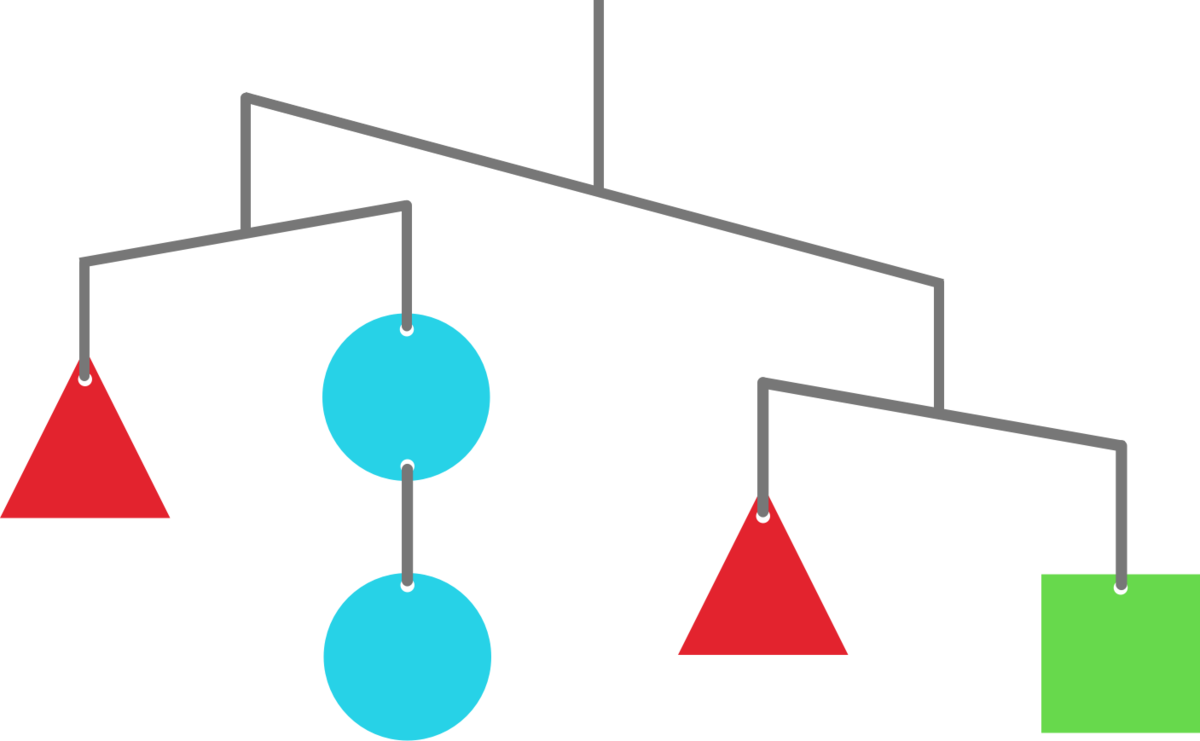The above shows how a mobile will be balanced when left to hang, and the rods are all tilted to the maximum degree.

Assuming that the fulcrum is at the center of each rod, what are the relative weights of these shapes?

Circle > Triangle > Rectangle Circle > Rectangle > Triangle Rectangle > Circle > Triangle Rectangle > Triangle > Circle Triangle > Rectangle > Circle Triangle > Circle > Rectangle

2 solutions

Chew-Seong Cheong
Apr 16, 2015

The left arm: $\triangle > \LARGE{\circ}$ $+\LARGE{\circ}$ $\quad \Rightarrow \triangle > \LARGE{\circ}$

The right arm: $\square > \triangle$

Therefore: $\boxed {\square > \triangle > \LARGE{\circ}}$

I chose the right answer, but said I was wrong

Jack Retherford - 5 months, 4 weeks ago

Sorry, I can't help you.

Chew-Seong Cheong - 5 months, 4 weeks ago

O+O>triangle
This is shown in figure how did you assume it. I have done it correct in another way.
Would you kindly explain your idea?

Irtaza Sheikh - 6 years, 1 month ago

I hope the picture help.

Chew-Seong Cheong - 6 years, 1 month ago

Oon Han
Jul 7, 2019

From the balance beam, the triangle weighs more than two circles, meaning that it weigh more than a circle. Thus, Triangle > Circle.

From the balance beam, square weighs more than a triangle. Thus, Rectangle > Triangle > Circle.

Putting these two inequalities together, we get $\boxed{\text{Rectangle > Triangle > Circle}}$ .

Therefore, the answer is Rectangle > Triangle > Circle .

Imbalance Puzzle - Part 3

2 solutions

0 pending reports