Tracking the height of a Baseball
The graph of the equation
h = -at
+ bt + c
which describes how the height, h, of a hit baseball changes over time, t, is show below.
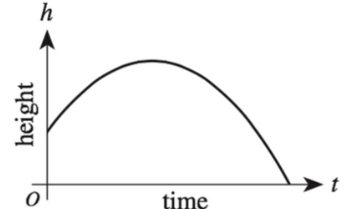If you alter only this equation’s c term, which gives the height at time t = 0, the alteration has an effect on which of the following?
- The h-intercept
- The maximum value of h
- The t-intercept
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The equation we are given h = -at 2 +bt + c is a parabola and we are told to describe what happens when we change c (the y-intercept).
From what we know about functions and function translations, we know that changing the value of c will shift the entire parabola upwards or downwards, which will change not only the y-intercept (in this case called the “h intercept”), but also the maximum height of the parabola as well as its x-intercept (in this case called the t intercept). You can see this in action when we raise the value of the y-intercept of our parabola.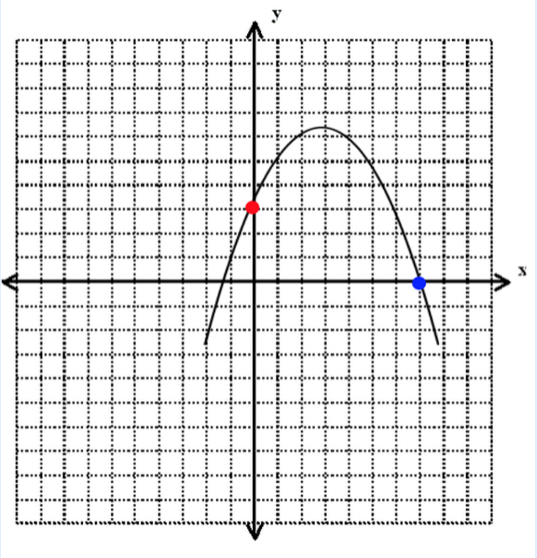
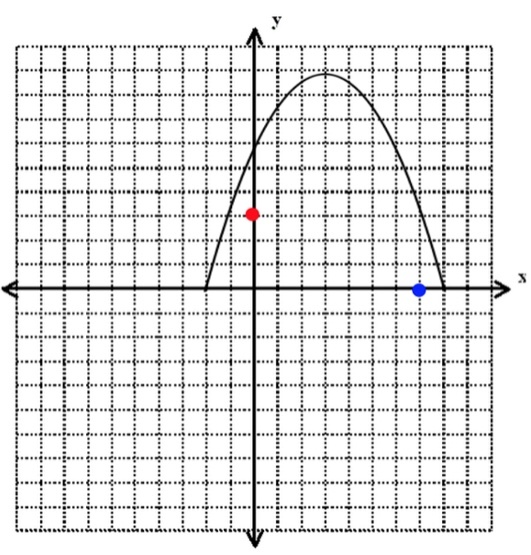
Options 1, 2, and 3 are all correct.